В статье рассматривается алгоритм построения цифрового генератора сигналов, приведены примеры описания генератора гармонических функций, линейной, экспоненциальной, степенной функции, генератора ЛЧМ-сигнала.
Ключевые слова : цифровой генератор, гармоническая функия, ЛЧМ- сигнал.
Генератор сигнала является одной из составных частей телекоммуникационных устройств. При цифровой обработке используются цифровые генераторы. Известно несколько вариантов реализации этого блока: табличный метод (значения отсчетов сигнала на периоде повторения), прямой цифровой синтез ( DDS ) [1], технология TrueForm компании Agilent Technologies [2] требуют значительных затрат памяти. Методы на основе аппроксимации требуют большого количества вычислений. Генератор на основе алгоритма CORDIC использует только операции сложения [3]. В статье предложен метод генерации цифрового сигнала, не требующий затрат памяти.
Пусть задана формула для отсчетов дискретного сигнала
f(n)= F(n).
Если
f(n)
можно представить как функцию
f(i), i
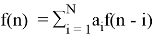
где a i — константы,
f(n-i) — N предыдущих отсчетов сигнала,
то зная значения f (0), f (1), …, f ( n-N ), можно получить значения f(n), используя рекурсивный фильтр, начальные значения регистров равны f(n-i).
Пусть
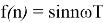
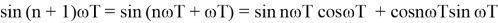
тогда можно записать
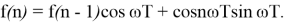
Причем
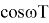
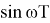
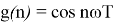
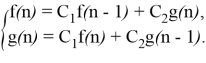
Представляя систему в виде схемы, получаем цифровой генератор синусоидального и косинусоидального сигнала с частотой
F
, соответствующей
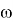
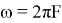
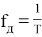
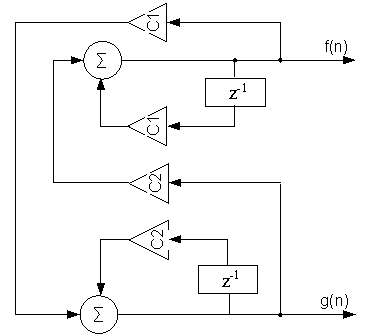
Рис. 1. Реализация алгоритма генератора синуса и косинуса
При реализации алгоритма в аппаратном базисе необходимо сформировать на выходах схемы начальные значения, соответственно
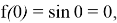
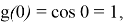
В регистры, обозначенные на схеме задержками (z -1 ), необходимо загрузить начальные значения
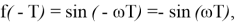
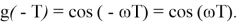
В общем случае получаем, если существует такой набор функций f 1 , f 2 , …, f K , каждую из которых можно представить в виде
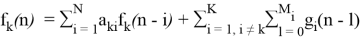
то можно реализовать цифровой генератор, формирующий отсчеты всех K функций f i , i =1… K .
Этому условию удовлетворяют гармонические функции (вывод приведен выше), экспонента, комплексная экспонента, степенная функция и все функции, которые можно представить через эти функции. Приведем вывод для некоторых функций.
Экспоненциальная функция f 1 (n)=e kn :
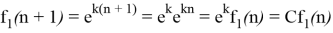
реализуется рекурсивным фильтром первого порядка.
Линейная функция f 2 (n)=kn+b :
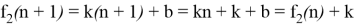
Частный случай f 3 (n)=n :
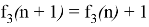
Реализация f 2 (n) — рекурсивный фильтр первого порядка с коэффициентом 1 и сумматор с константой k .
Квадратичная функция f 4 (n)=n 2 :
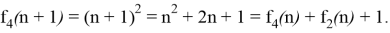
Для реализации квадратичной функции необходимо использовать генератор линейной функции f 2 (n) c k =2 и b =0.
Кубическая функция f 5 (n)=n 3 :
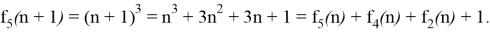
Для реализации кубической функции необходимо использовать генераторы квадратичной и линейной функций.
Очевидно, что для генерации степенной функции n k потребуются генераторы степенных функций меньшего порядка, вплоть до линейной. Аналогично реализуется генератор функции, задаваемой полиномом произвольного порядка.
Рассмотрим возможность реализации генератора сигнала с линейной частотной модуляцией (ЛЧМ). ЛЧМ-сигнал задается формулой
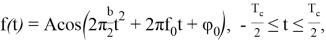
где Т с — длительность сигнала,
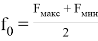
F макс — максимальная частота сигнала,
F мин — минимальная частота сигнала,
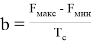
φ 0 — начальная фаза.
При рассмотрении цифрового ЛЧМ-сигнала Т с — длительность символа модуляции. Выражение для отсчета цифрового сигнала имеет вид (начальную фазу примем равную 0, частоту дискретизации и амплитуду А — равными 1, обозначим
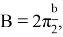
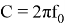
тогда можно записать
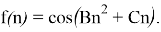
Найдем f(n+1):
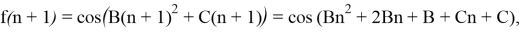
Выделим аргумент, соответствующий f(n)
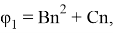
оставшуюся часть аргумента обозначим
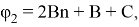
тогда
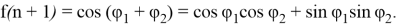
Рассмотрим составляющие этого выражения:
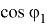
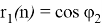
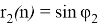
Для нахождения
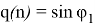
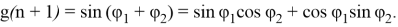
Представим r 1 (n) и r 2 (n) аналогично
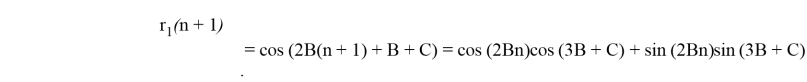
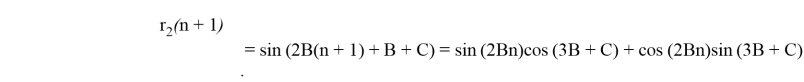
Таким образом, получили, что для нахождения сигнала по формуле (3), необходимо иметь квадратурную функцию ЛЧМ- сигнала, а также — синус и косинус с аргументом 2Bn , для их определения можно воспользоваться системой (1) и схемой рисунка 1.
Цифровой генератор ЛЧМ-сигнала описывается системой уравнений
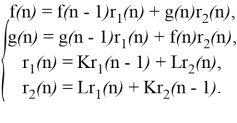
Рассмотренные алгоритмы были реализованы в среде Matlab , показали свою работоспособность. Алгоритмы содержат только операции сложения и умножения, затраты памяти невелики. Например, для реализации рассмотренных генераторов не требуются аппаратные блоки памяти, используется небольшое число регистров.
Литература:
- Тюрин В. А. Метод прямого цифрового синтеза в генераторах сигналов специальной формы SFG-2110 и АКИП-3410/3: учебно-методическое пособие / В. А. Тюрин. — Казань: Казанский федеральный университет, 2015. — 74 с.
- Технология генерации сигналов Trueform компании Agilent. Технический обзор. — Текст: электронный // URL:http://www.unitest.com/pdf/TrueForm — 5991–0852RURU.pdf (дата обращения: 24.04.2020).
- Благодаров А. В., Целочисленный алгоритм генерации синусоидального сигнала. — Цифровая Обработка Сигналов № 4. 2017. С. 69 -84.
- Гольденберг Л. М. Цифровая обработка сигналов: Справочник/ Л. М. Гольденберг и др. — М.: Радио и связь. 1985. — 312 с.







