Задача адресной перевозки с временными окнами

Задача адресной перевозки состоит в составлении маршрутов и расписании транспортных средств для перевозки людей “от двери до двери”. С такой задачей сталкиваются службы такси, школьные автобусы и социальные службы специального транспортного обслуживания. В данной работе рассматривается статическая задача адресной перевозки с временными окнами и одним транспортным средством. Для решения поставленной задачи использовались различные вариации алгоритма муравьиной колонии. Проведено сравнение работы алгоритмов на тестовых данных.

Ключевые слова: задача адресной перевозки, муравьиный алгоритм.

Введение. Темой данной работы является задача адресной перевозки (Dail-a-Ride Problem или DARP) с временными окнами. DARP относится к классу задач вывоза и доставки, однако в отличии от остальных задач данного класса, она связана с перевозкой людей, а не товаров. С задачей адресной перевозки сталкиваются службы такси, школьные автобусы и социальные службы специального транспортного обслуживания, занимающиеся перевозкой пожилых и маломобильных людей.

Постановка задачи. В данной работе рассматривается задача с одним транспортным средством, которое начинает и заканчивает свой маршрут в депо. Транспортное средство не может выполнять несколько заказов одновременно, то есть забирать людей “по дороге”. Перевозка осуществляется по заранее известным запросам, включающим следующие данные: 1) координаты отправления и прибытия, 2) временные окна на вывоз или доставку (то есть максимальное и минимальное время начала и окончания поездки), 3) время на обслуживание клиента до и после поездки (если клиенту требуется дополнительное время, чтобы сесть в машину или загрузить багаж).

Математическая постановка. Задачу адресной перевозки можно задать на графе G=(N, A) , где N — множество вершин: P={ 1 ,…,n} и D={n+ 1 ,…, 2 n} — вершины отправления и прибытия соответственно, {0} — вершина, обозначающая депо, в котором изначально находятся все транспортные средства, а A — множество ребер. Каждый маршрут клиента i начинается в вершине и заканчивается в вершине . Кроме того, для каждой вершины известно время c _i на обслуживание клиента перед или после поездки и временное окно [ e _i , l _i ]. Для каждой дуги известно время t _ij пути по ней.

(2)

(3)

(4)

(5)

(7)

(8)

(9)

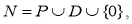
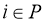
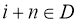
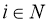
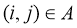
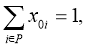
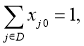
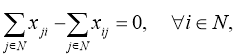
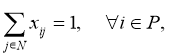
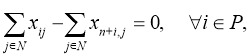
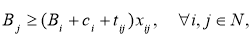
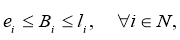
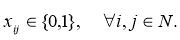
Целевая функция (1) минимизирует общую стоимость маршрута, которая в данном случае является временем. Ограничения (2), (3) и (4) гарантируют, что все маршруты транспортного средства начинаются и заканчиваются в депо. Условия (5) и (6) устанавливают, что каждый заказ будет выполнен один раз, и транспортное средство переместится из вершины отправления в соответствующую ей вершину доставки. Ограничения на время прибытия в следующую вершину маршрута B _i задано в неравенстве (7). Условие (8) ограничивает время прибытия минимальным и максимальным временем начала обслуживания вершины. Наконец, в условии (9) полагаем, что x _ij =1, если транспортное средство переместилось из вершины i в вершину j , и x _ij =0 в ином случае.

Алгоритм решения. Для решения задачи адресной перевозки, поставленной в данной работе, было решено использовать метаэвристический алгоритм муравьиной колонии. В общем случае алгоритм муравьиной колонии для решения задачи адресной перевозки выглядит следующим образом.

1. Инициализация параметров.
2. Расстановка муравьев по вершинам в случайном порядке.
3. for t = 1 to t_max do
4. for k = 1 to m do
5. for i = 1 to n — 1 do
6. применение стратегии выбора пути;
7. обновление феромонов;
8. поиск лучшего маршрута;
9. Вывод глобально лучшего маршрута.

Здесь t_max — заранее заданное число повторов основной части алгоритма (или жизненный цикл муравьиной колонии), m — количество муравьев в колонии, n — количество вершин в графе.

Есть несколько стратегий выбора пути ─ Ant System (AS) [1], Ant Colony System (ACS) [2] и Modified Ant Colony System (M — ACS). Применяя данные стратегии, муравьи опираются на следующую информацию — количество феромона ij на ребре ( i, j ), видимость ij вершины j и список посещенных вершин tabu_list.

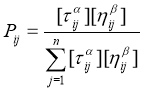
ACS :

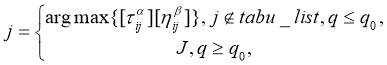
M - ACS :

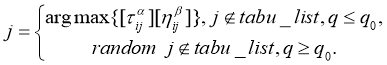
Также существуют различные способы вычисления видимости вершины. В данной работе рассмотрены несколько подходов, учитывающих временные окна. Для удобства обозначим их как ANT_TIME 1 [3], ANT_TIME 2 [4] и ANT_TIME 3 [5].

ANT-TIME 1

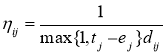
ANT-TIME 2

,

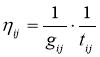
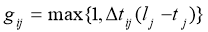
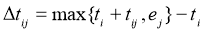
ANT-TIME 3

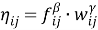
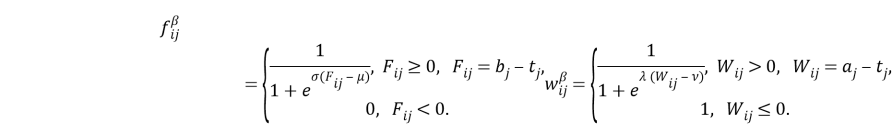
Для решения поставленной задачи использовались алгоритмы ANT_TIME 1, ANT_TIME 2 и ANT_TIME 3 в связке с каждой из стратегий выбора пути AS, ACS и M-ACS. Стоит отметить, что подходы ANT_TIME 2 и ANT_TIME 3 впервые использовались для решения задачи адресной перевозки.

Алгоритмы были реализованы с использованием следующих значений параметров: n = 41 - количество вершин графа, m = 20 — количество муравьев в колонии, α = 1, β = 1, γ = 1 — параметры, отвечающие за влияние концентрации феромона и видимости на вероятность перехода, Q = 1 — количество феромонов, ω = 0.5 — параметр локального испарения феромона, ρ = 0.6 - параметр глобального испарения, σ = 0.01, λ = 0.01 — параметры для вычисления эвристик, q0 = 0.7 — параметр для выбора правила для перехода в следующую вершину в стратегиях ACS и M-ACS, ν = 60 — скорость, t _max = 20 — жизненный цикл муравьиной колонии.

Для получения средних значений каждый алгоритм запускался 100 раз. В таблице 1 представлены результаты работы алгоритмов для одной из тестовых выборок.

Таблица 1

Результаты работы алгоритмов на графе с 41 вершиной

Ни в одном из запусков алгоритма ANT-TIME 1 не было найдено маршрутов, построенных с соблюдением всех временных окон, поэтому лучшее время приводится для максимального количества обслуженных заказов. Данный алгоритм показал худшие результаты относительно количества успешных туров, однако время работы алгоритма ANT-TIME 1 значительно меньше времени работы остальных алгоритмов. Это связано с малым количеством операций для вычисления эвристик.

С помощью алгоритмов ANT-TIME 2 и ANT-TIME 3 удалось построить маршруты, удовлетворяющие всем ограничениям. Лучшее время маршрута, построенного алгоритмом ANT-TIME 2, было найдено с использованием стратегии ACS. То же можно сказать и о количестве успешных туров.

В алгоритме ANT-TIME 3 использовались эвристики, направленные на строгое соблюдение временных окон, этим объясняется достаточно большое количество успешных туров. При этом использование стратегии M-ACS позволило достичь лучших результатов как по времени лучшего маршрута, так и по количеству успешных маршрутов. В то же время ANT-TIME 3 требует наибольшего времени вычисления.

Таким образом, наилучшие результаты по значению целевой функции и времени работы показал алгоритм ANT-TIME 2 с использованием стратегии ACS, а количество успешных туров — алгоритм ANT-TIME 3 в связке со стратегиями M-ACS.

Алгоритмы ANT-TIME 2 ACS и ANT-TIME 3 M-ACS, показавшие наилучшие результаты, были дополнительно рассмотрены на графе со 101 вершиной (50 запросов на перевозку). Результаты представлены в таблице 2.

Таблица 2

Для трех тестовых наборов ANT-TIME 2 ACS не смог построить маршруты с соблюдением всех ограничений, в то время как ANT-TIME 3

M-ACS построил 1–3 успешных тура для каждого из пяти наборов данных. Однако, для наборов 4P1 и 5P1, в которых удалось обслужить всех клиентов, ANT-TIME 2 ACS показал лучшее время маршрута. Кроме того, ANT-TIME 2 ACS позволил включить в маршрут в среднем большее количество клиентов. Стоит также отметить, что время работы алгоритма ANT-TIME 2 ACS на используемых данных в среднем в 1.7 раз меньше времени работы ANT-TIME 3 M-ACS.

Заключение. В данной работе была рассмотрена статическая задача адресной перевозки с временными окнами и одним транспортным средством. В качестве основного метода решения был выбран алгоритм муравьиной колонии. По результатам исследования выявлены алгоритмы, строящие маршрут с наибольшим количеством обслуженных заказов — ANT-TIME 2 и ANT-TIME 3. Кроме того, для каждого из алгоритмов найдена стратегия перехода, с помощью которой можно получить наилучшее значение целевой функции. Сравнение этих алгоритмов на тестовых данных большей размерности позволило определить метод, позволяющий получить лучшее время маршрута. Таким алгоритмом является ANT-TIME 2 со стратегией ACS.

Литература:

1. Colorni A., Dorigo M., Maniezzo V. Distributed optimization by ant colonies // European Conference on Artificial Life, 1991.
2. Dorigo M. Gambardella L. M. Ant colony system: a cooperative learning approach to the traveling salesman problem // IEEE Transactions on Evolutionary Computation, 1997. Vol. 1, No 1, P. 53─66.
3. Tripathy T., Nagavarapu S. C., Azizian K., Pandi R. R., Dauwels J. Solving dial-a-ride problems using multiple ant colony system with fleet size minimisation // Advances in Computational Intelligence Systems, 2017. P. 325─336.
4. Baran B. and Schaerer M. A multiobjective ant colony system for vehicle routing problem with time windows // The 21st IASTED International Multi-Conference on Applied Informatics, 2003. P. 97─102.
5. Cheng C. B., Mao C. P. A modified ant colony system for solving the traveling salesman problem with time windows // Mathematical and Computer Modeling, 2007. Vol. 46. P. 1225─1235.
6. The VRP Web [Электронный ресурс]. URL: http://www.bernabe.dorronsoro.es/vrp/ (дата обращения: 10.01.2020).