Получены размеры звеньев манипулятора с помощью составленных для данного механизма функций расчета обратной кинематики. Определены исходные данные в системе MATLAB для дальнейшего подбора редуктора (червячного) с использованием метода, базирующегося на матрице Якоби.

Ключевые слова: механизм, степень свободы, программный комплекс, матрица Якоби.

Данный механизм содержит 6 цепей. Каждая цепь состоит из: вертикально ориентированной призматической пары, 2-х сферических шарниров, и соединяющих эти шарниры промежуточных звеньев. Область манипулирования: ± 0,15 м по осям x и у, ± 0,1 м по оси z и ± 20 ° угол поворота по любой оси.

Положение и ориентация выходного звена описывается шестью выходными координатами: координаты x, y, z точки D в неподвижной системе Oxyz задают положение, а углы поворота φ_x, φ_y, φ_z в подвижной системе Dx'y'z' — ориентацию. При этом ориентация самой системы Dx'y'z' считается неизменной, то есть оси x', y' и z' всегда остаются параллельны осям x, y и z.

Для использования данной методики предварительно были подобраны размеры звеньев механизма с использованием функций, которые решают обратную задачу кинематики для одной цепи и для всего механизма. Представим полученную конструкцию на рисунке 1.

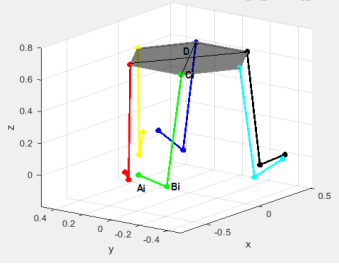
Рис.1. Отрисовка механизма, полученная в результате выполнения созданной программы в MATLAB

Геометрические размеры (м):

– l, длины звеньев (одинаковы для всех цепей):

l_AB = 0,2, l_BC = 0,7;

– h, пределы перемещения каретки (одинаковы для всех цепей): h_min = 0,6, h_max = 0,8;

– x_A, координаты, определяющие положение и ориентацию вертикальной стойки механизма и звена AB:

x_A1 = 0,3155, y_A1 = — 0,4505, x_B2 = 0,3155, y_B2 = 0,4505, x_A3 = 0,2224, y_A3 = 0,4985, x_A4 = — 0,5548, y_A4 = 0,0479, x_A5 = — 0,5548, y_A5 = — 0,0479, x_A6 = 0,2324, y_A6 = — 0,4985, для всех цепей z_A = 0,05;

– координаты точек Сi в начальном положении в системе Dx'y'z':

x'_C01 = 0,3155, y'_C01 = — 0,1821, x'_C02 = 0,3155, y'_C02 = 0,1821, x'_C03 = 0, y'_C03 = 0,3643, x'_C04 = — 0,3156, y'_C04 = 0,1821, x'_C05 = — 0,3155, y'_C05 = — 0,1821, x'_C06 = 0, y'_C06 = — 0,3643, для всех цепей z'_C0 = 0;

– углы поворота плоскостей звеньев АВ, рад:

α_AB1 = — 1,5708, α_AB2 = 1,5708, α_AB3 = 0,5236, α_AB4 = — 3,6652, α_AB5 = 2,6180, α_AB6 = 5,7596.

Для определения данных, необходимых для подбора червячного редуктора, был использован метод, базирующийся на матрице Якоби, так как практически для любого механизма параллельной структуры c n степенями свободы можно получить аналитические уравнения связи в виде n неявных функций Fi(x₁,..., x_n, q_аi)(i=1...n) от координат выходного звена x₁,...,x_n и перемещений в активных парах q_а1,...,q_аn. В данном случае пренебрегаем инерцией по той причине, что в данном механизме нет больших ускорений. Тогда, дифференцируя по времени указанные выше функции, получим систему линейных уравнений:

Количество уравнений при этом равно числу степеней свободы механизма n, N_a — число активных пар механизма. Указанная система в матричной форме после переноса в правую часть скоростей в активных парах q̇_аi, будет иметь следующий вид:

,

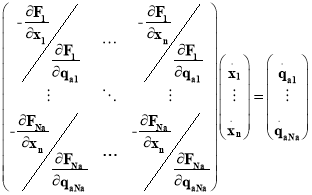или иначе

.

В нашем случае функция F имеет выражение:

.

А обратная матрица Якоби (размер 6 × 6):

, где производные вычисляют в отдельной программе, представленной на рисунке 2. По индексу определяем значение координат и углов цепи, которые необходимо подставить в соответствующую производную).

Рис.2. Программа вычисляющая производные

Для определения линейной скорости в приводах необходимо вычислить норму i-й строки с 1-го по 3-й элемент включительно, а угловой скорости с 4-го по 6-й включительно.

Например, для поиска линейной скорости 1-й цепи соответственно необходимо выполнить следующее:

По аналогичной зависимости рассчитываются скорости для других цепей. Из полученных значений линейных и угловых скоростей выбираем наибольшие и находим максимальную скорость вращения выходного вала. Для поиска усилий необходимо транспонировать матрицу Якоби, а дальше следовать тем же указаниям, что и для поиска скоростей в приводах. Фрагменты программ представлены на рисунке 3.

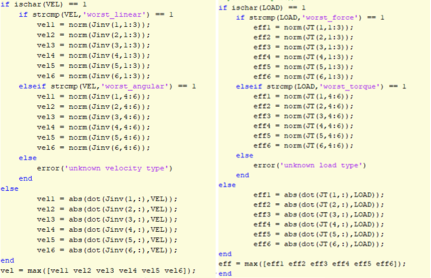
Рис. 3. Фрагменты программ для поиска скоростей и усилий

В результате анализа рабочей зоны, были получены следующие значения максимального момента и максимальной частоты вращения вала редуктора:

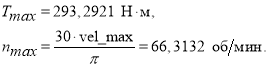
Литература:

1. Ларюшкин П. А., Глазунов В. А., Эрастова К. Г. Определение максимальных усилий в приводах манипуляторов параллельной структуры по заданной величине внешней нагрузки. Машиностроение и инженерное образование, 2016, № 2(47), с. 40–46.
2. Эрастова К. Г., Ларюшкин П. А. Рабочие зоны механизмов параллельной структуры и способы определения их формы и размеров // Известия высших учебных заведений. Машиностроение. — 2017. — № 8. — С. 78–87.
3. Хейло С. В., Ларюшкин П. А., Глазунов В. Г., Эрастова К. Г. Определение рабочей зоны манипуляторов параллельной структуры. Справочник. Инженерный журнал с приложением, 2013, № 2(191), с. 27–31.