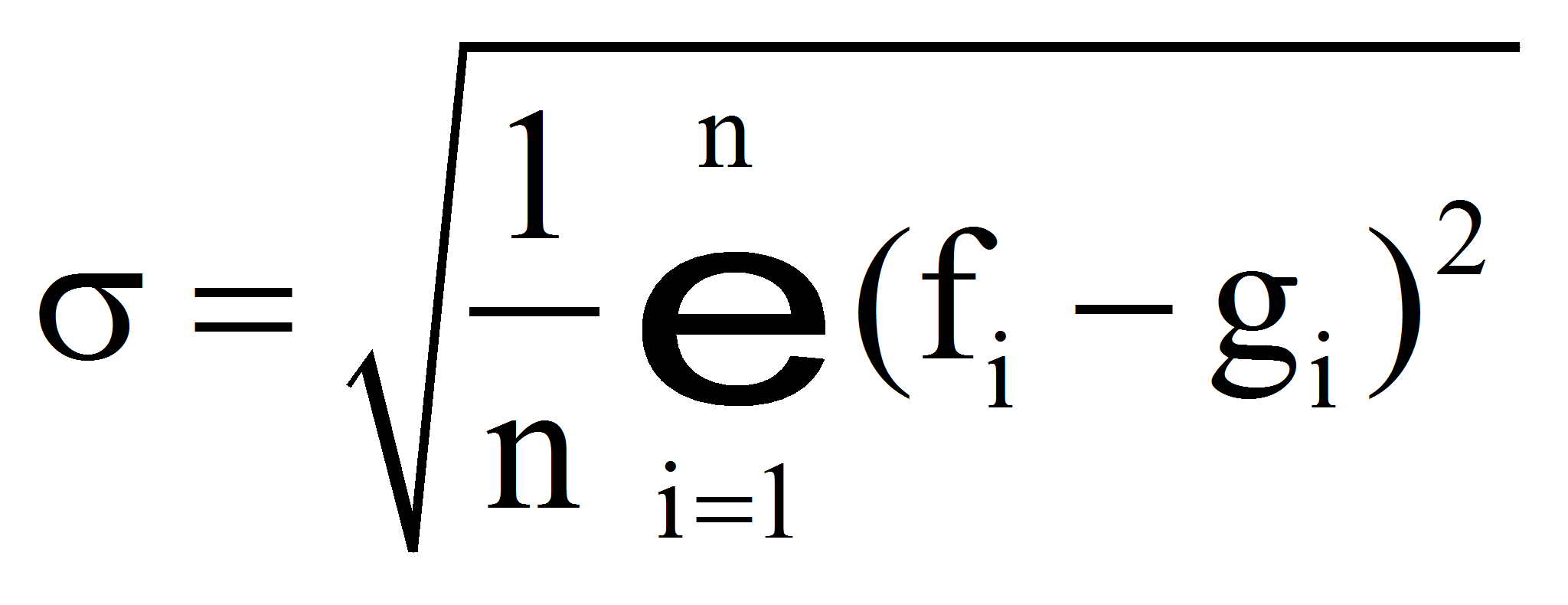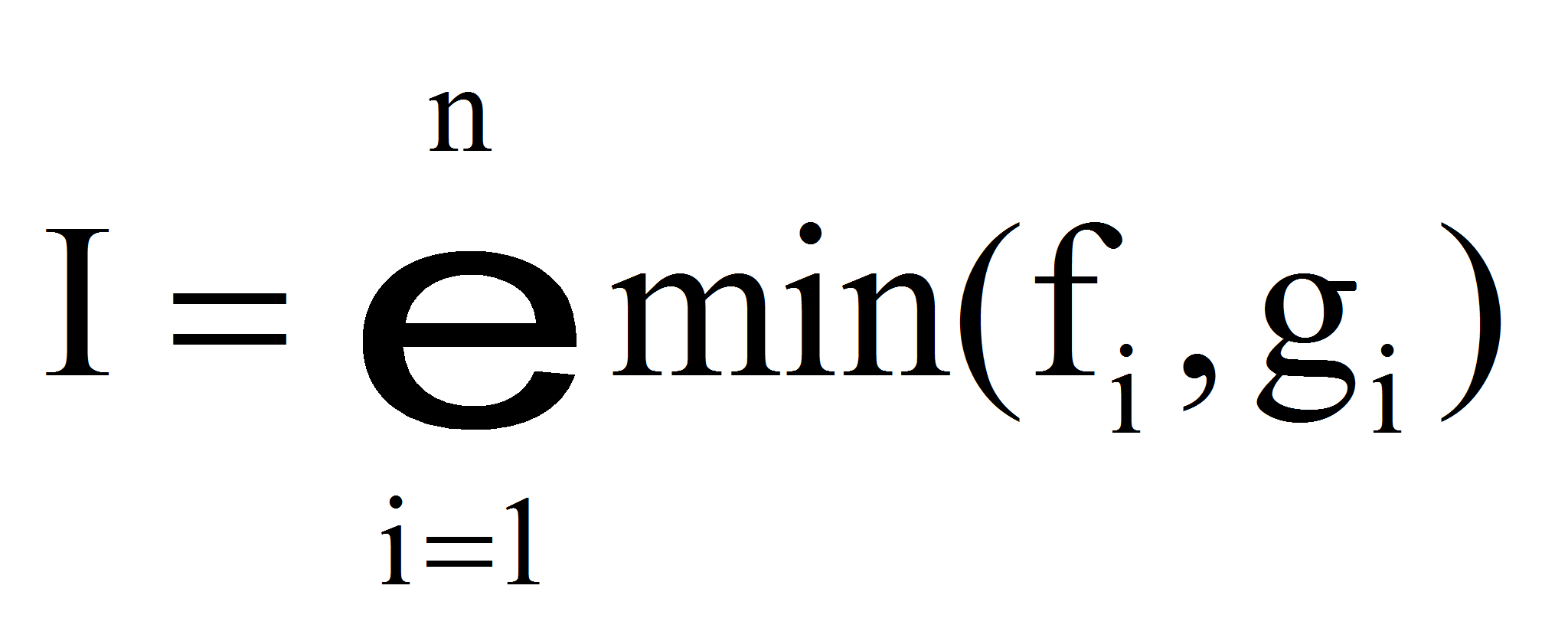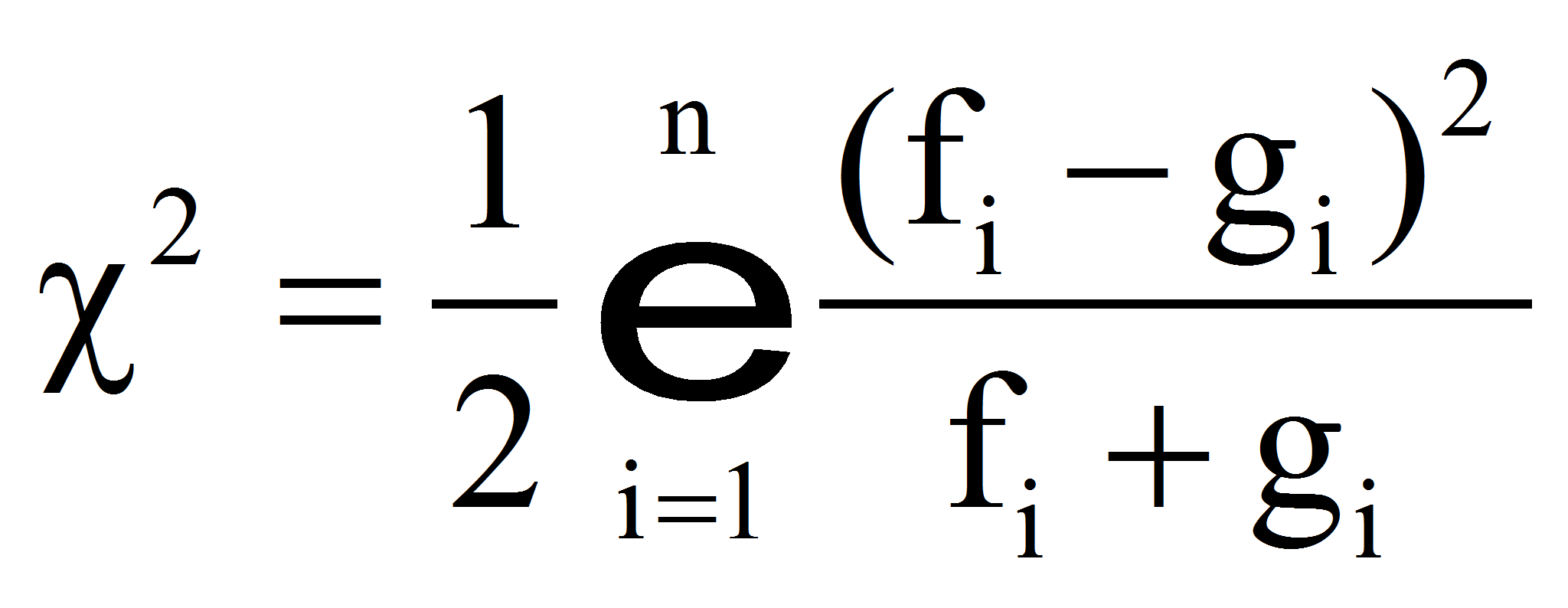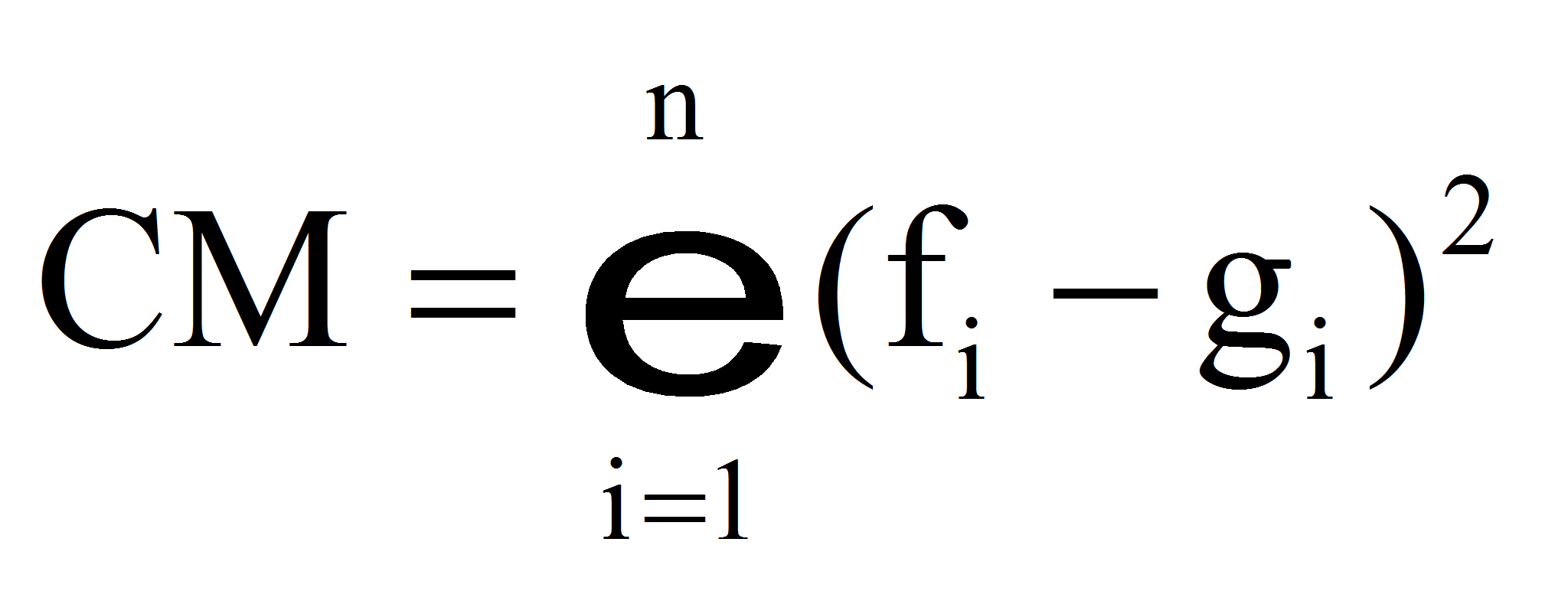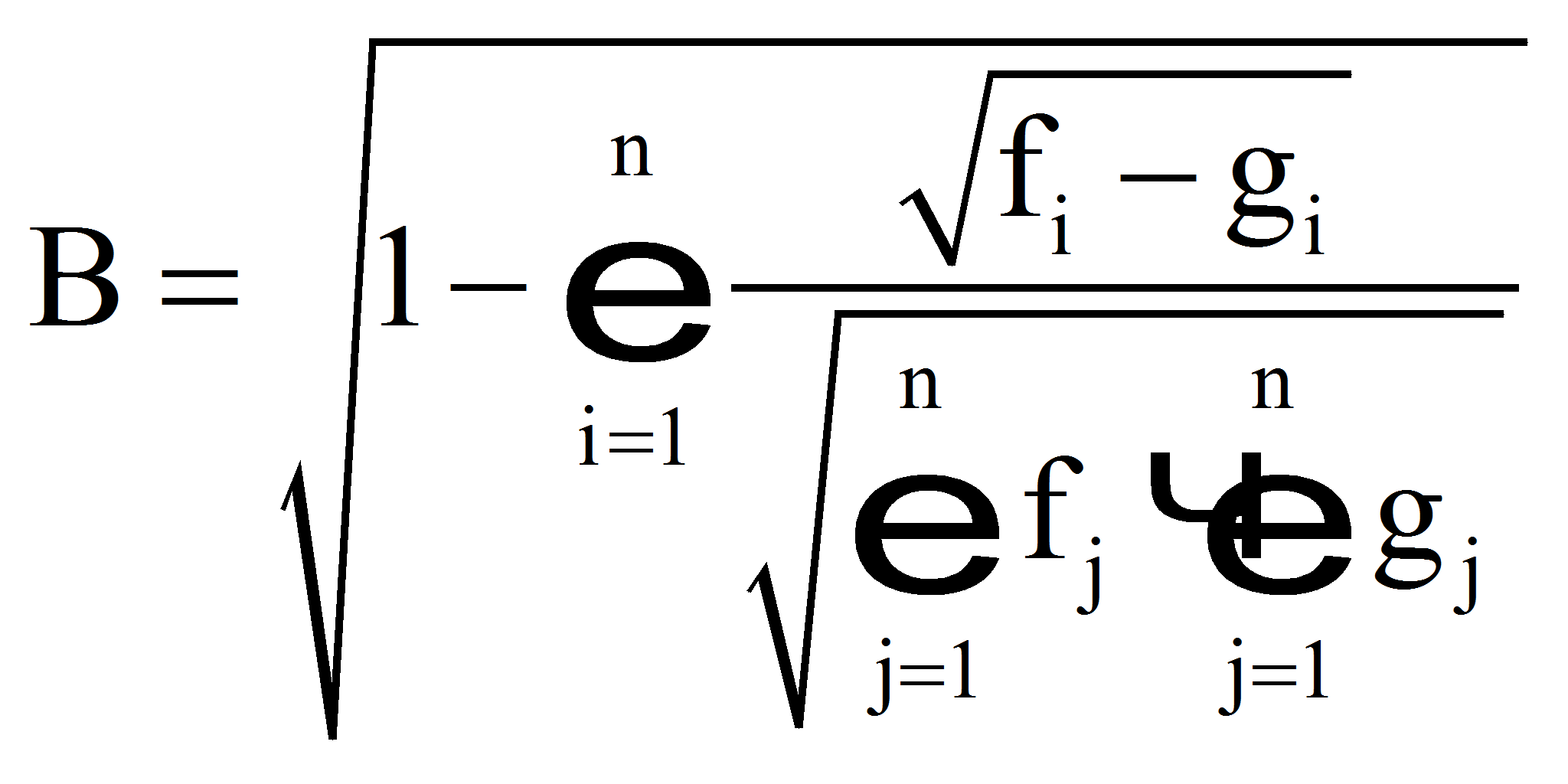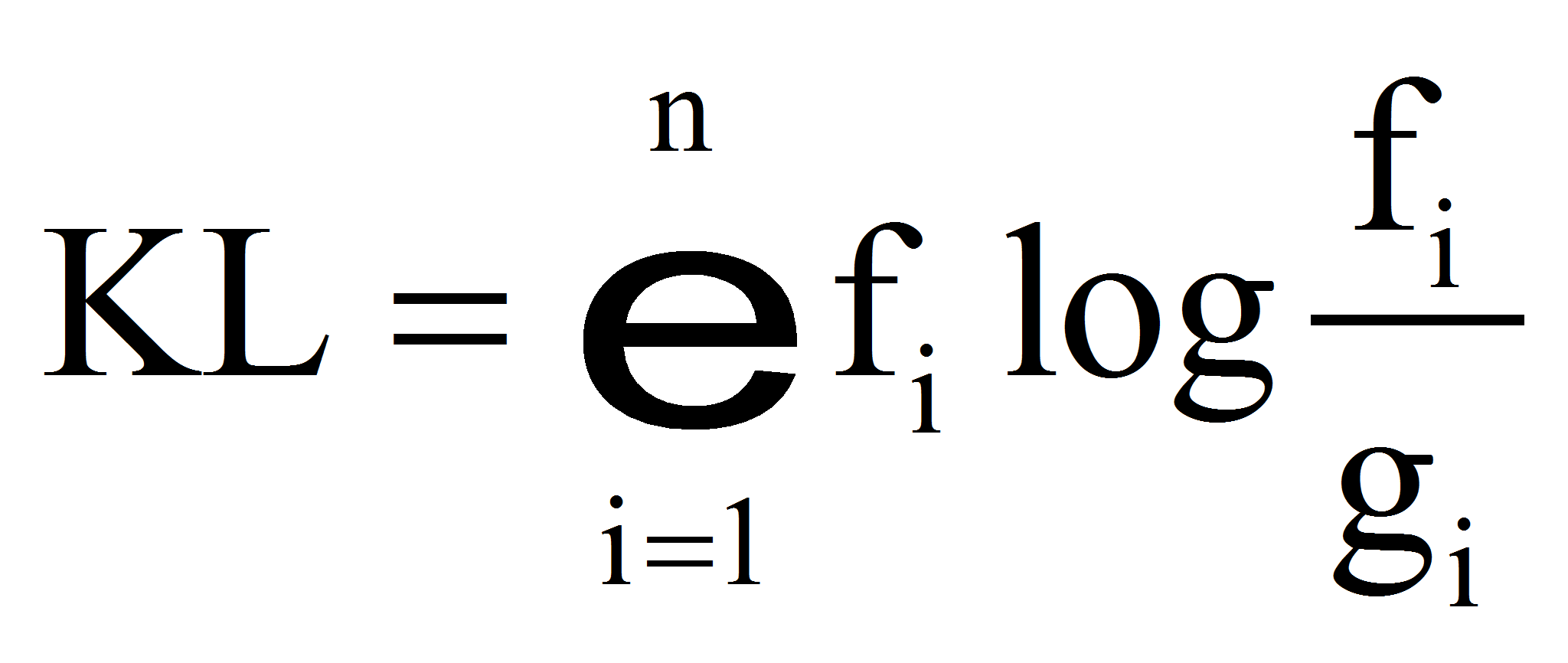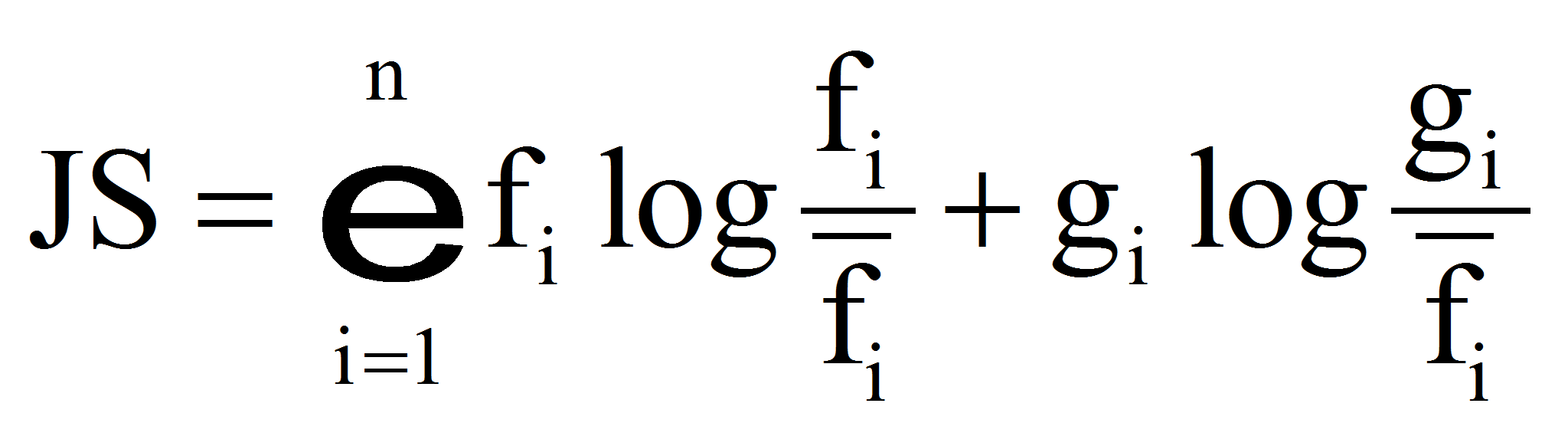Сравнение трехмерных объектов. Критерии оценки сходства

В данной работе описана задача сравнения полигональных моделей тела человека. Задача была сформулирована в рамках определения точности методов моделирования сложных объектов, таких как тело человека.

Сравнению подвергались объекты, полученные с применением концепции порождающих моделей (деформация базовой модели для набора параметров) и результаты трехмерного сканирования. Оба объекта были представлены в полигональном виде, в качестве полигона использовался треугольник. Сравнение осуществлялось с помощью стохастических методов, с использованием функций формы.

В тех случаях, когда необходимо сопоставить два трехмерных объекта, часто прибегают к сравнению их дескрипторов формы – однозначно характеризующих подписей (значений). Их же, в свою очередь, получают с помощью функций формы, которые отражают связи, отношения между точками на поверхности фигуры.

К функциям формы обычно предъявляются некоторые требования. В идеале полученное с их помощью распределение форм должно быть инвариантно относительно преобразований подобия и тесселяции (увеличение количества полигонов) и оно должно быть нечувствительным к шуму, трещинам и вставкам (удалениям) мелких полигонов.

В общем случае может быть выбрана любая функция. Полезными, например, будут те, которые включают предметно-ориентированные знания. К ним относятся доступность информации (расстояние между случайными, но взаимно видимыми точки) или параметры поверхности (цвет, текстурные координаты, нормали и кривизна). Однако чаще всего используются функции, в основе которых лежат геометрические измерения (например, углы, расстояния, площади и объемы) [1, 2].

В качестве функции, описывающей форму объекта, в данной работе было выбрано евклидово расстояние между парами случайных точек на поверхности объекта, вычисляемое по формуле:

,

где x₁, y₁, z₁ – координаты первой точки, x₂, y₂, z₂ – координаты второй точки.

При выборе функции формы возникает вопрос: как вычислить ее распределение. Для этого используются стохастические методы, определяются N значений функции формы и строится гистограмма путем подсчета – сколько образцов попало в каждый из заданных заранее интервалов. Из гистограммы восстанавливается кусочно-линейная функция, которая является функцией плотности распределения.

Таким образом, взяв одинаковое количество точек N из двух множеств (точек на поверхности объектов) и рассчитав для каждой из них евклидово расстояние от нее до всех других, мы получили множество расстояний внутри объекта S, их количество будет определяться формулой:

.

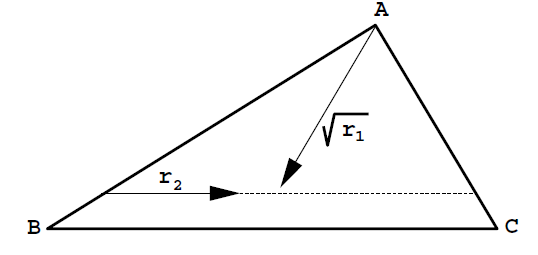
Для такого подхода необходимо, чтобы объект был представлен множеством точек, а не полигональной структурой. Приведение модели к точечной форме проходило путем замены полигона на точку. Полигоном для сравниваемых объектов являлся треугольник. Сначала для каждого треугольника вычислялась его площадь. Далее случайным образом выбирались треугольники с вероятностью пропорциональной площади, т.е. генерацией случайных чисел от 0 до суммарной площади фигуры. Для каждого выбранного треугольника с вершинами А, B, C определялась точка на его поверхности с использованием двух случайных величин r₁ и r₂, изменяющихся от 0 до 1, по следующей формуле [3]:

,

где A, B и C – это стороны треугольника, r₁ – случайная величина, расстояние от вершины A в направлении противолежащей стороны, r₂ – случайная величина, сдвиг точки параллельно этой же противолежащей стороне (рисунок 1).

Рисунок 1 – Выбор случайной точки в треугольнике

Построив форму распределения для двух 3D-моделей, осталась нерешенной задача определения меры их сходства. Есть много стандартных способов сравнения двух функции f и g, представленных вероятностями распределения. В данной работе использовалось восемь показателей: среднеквадратическое отклонение, пересечение, критерий хи-квадрат, критерий Колмогорова-Смирнова, критерий Крамера-Мизеса, Критерий Бхаттачария, дивергенция Кульбака-Лейблера, дивергенция Дженсена-Шеннона [4, 5]. Ниже приведены формулы для расчета этих показателей, где n – объем выборки; f_i(j) – количество наблюдений в i-м (j-м) интервале первой выборки; g_i(j) – количество наблюдений в i-м (j-м) интервале второй выборки; .

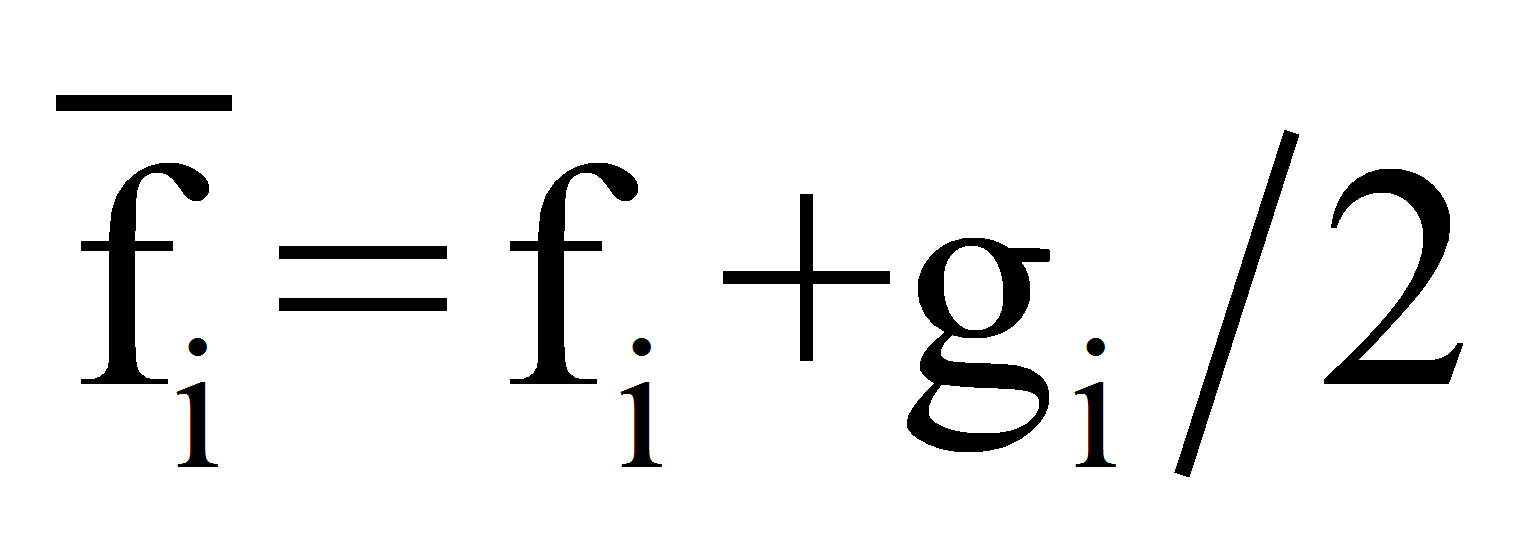Среднеквадратичное отклонение

Пересечение

Критерий хи-квадрат

Критерий Колмогорова-Смирнова

Критерий Крамера-Мизеса

Критерий Бхаттачария

Дивергенция Кульбака-Лейблера

Дивергенция Дженсена-Шеннона

Все из приведенных выше показателей, за исключением критерия Бхаттачария, будут равны 0 при абсолютном совпадении двух функций плотности распределения. Так как критерий Бхаттачария изменяется от 0 до 1, можно ввести суммарный критерий оценки, вычисляемый по формуле:

,

чем он ниже, тем объекты более схожи.

Таким образом, применительно к моделированию трехмерных объектов с помощью порождающих моделей, можно предложить следующий подход: рассчитав суммарный показатель для базовой модели и результата трехмерного сканирования, получить границы изменения этого показателя для данного объекта, в нашем случае манекена. Затем, создавая параметрическую модель путем деформации базовой, показатель будет изменяться и характеризовать точность моделирования.

1. Osada, R. Shape Distributions / R. Osada, T. Funkhouser, B. Chazelle // ACM Trans. on Graph. – 2002. – Vol. 21, № 4. – P 807–832.
2. Ohbuchi, R. Shape-similarity search of 3D models by using enhanced shape functions / R. Ohbuchi, T. Minamitani, T. Takei // International Journal of Computer Applications in Technology (IJCAT). – 2005. – Vol. 23, № 2/3/4. – P 70–85.
3. Osada, R. Matching 3D Models with Shape Distributions / R. Osada, T. Funkhouser, B. Chazelle, D. Dobkin // SMI 2001 International Conference on. – 2001. – P 154–166.
4. Rubner, Y. Empirical evaluation of dissimilarity measures for color and texture / Y. Rubner , J. Puzicha, C. Tomasi, J. Buhmann. // IEEE International Conference on Computer Vision. – 1999. – P 1165–1173.
5. Bhattacharyya, A. On a measure of divergence between two statistical populations defined by their probability distributions / A. Bhattacharyya // Bulletin of the Calcutta Mathematics Society. – 1943. – 35:99–110.