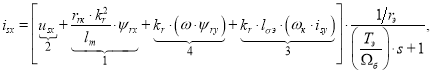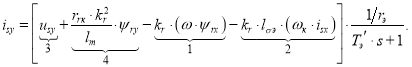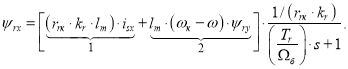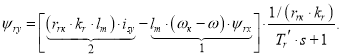Для сравнения с результатами математического моделирования линейного асинхронного двигателя в Matlab-Script дадим модель асинхронного двигателя в Script.
В работе [1] была получена структурная схема для определения статорного тока isx в Simulink-Script (рис. 1) по следующему уравнению:
|
|
(1) |
где ![]() - электрическая скорость вращения ротора;
- электрическая скорость вращения ротора;
![]() - механическая угловая скорость на валу двигателя.
- механическая угловая скорость на валу двигателя.
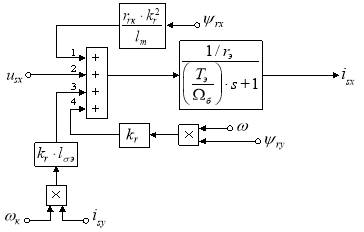
Рис. 1. Структурная схема для определения тока isx в Simulink-Script
Преобразуем уравнение (1) для программирования в Matlab-Script:
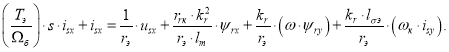
Обозначим ![]() , тогда:
, тогда:
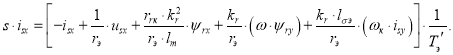
Переходим к оригиналу ![]() :
:
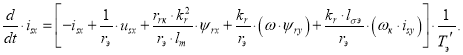
Переходим к конечным разностям (метод Эйлера):
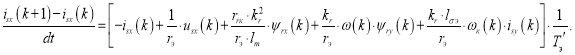
Отсюда ток isx в Matlab-Script определится следующим образом:
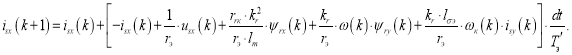
Уравнение для определения тока isy в Simulink-Script, полученное в работе [1], имеет следующий вид:
|
|
(2) |
Структурная схема реализации уравнения (2) приведена на рис. 2.
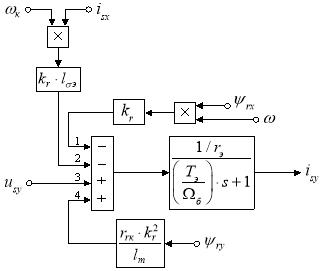
Рис. 2. Структурная схема для определения тока isy в Simulink-Script
Аналогично преобразуем выражение тока isy в форму, удобную для программирования в Matlab-Script:
![]()
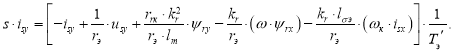
Переходим к оригиналу:
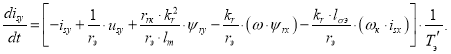
Переходим к конечным разностям:
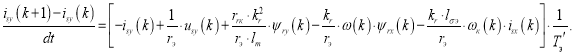
Ток isy в Matlab-Script определится следующим образом:
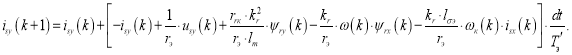
В работе [1] была получена структурная схема для определения потокосцепления ψrx в Simulink-Script (рис. 3) по следующему уравнению:
|
|
(3) |

Рис. 3. Структурная схема для определения потокосцепления ψrx в Simulink-Script
Преобразуем уравнение (3) для программирования в Matlab-Script:
![]()
Обозначим ![]() , тогда:
, тогда:
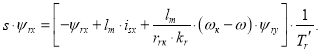
Переходим к оригиналу:
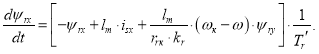
Переходим к конечным разностям:
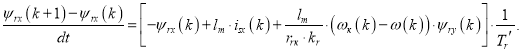
Отсюда потокосцепление ψrx в Matlab-Script определится следующим образом:
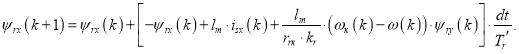
Уравнение для определения тока ψry в Simulink-Script, полученное в работе [1], имеет следующий вид:
|
|
(4) |
Структурная схема реализации уравнения (4) приведена на рис. 4.
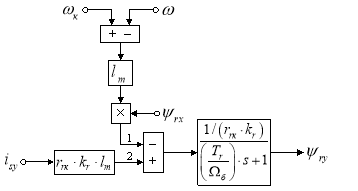
Рис. 4. Структурная схема для определения потокосцепления ψry в Simulink-Script
Преобразуем выражение потокосцепления ψry в форму, удобную для программирования в Matlab-Script:
![]()
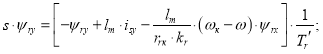
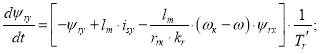
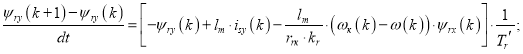
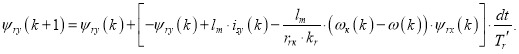
На рис. 5 представлена структурная схема для реализации уравнения электромагнитного момента в Simulink-Script:
![]()
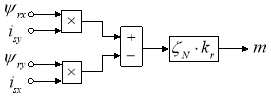
Рис. 5. Математическая модель определения электромагнитного момента m в Simulink-Script
Уравнение электромагнитного момента для реализации в Matlab-Script:
![]()
Механическая угловая скорость вращения вала двигателя в Simulink-Script (рис. 6):
![]()
![]()
Рис. 6. Математическая модель определения механической угловой скорости вращения вала двигателя в Simulink-Script
Отсюда механическая угловая скорость вращения вала двигателя в Matlab-Script:
![]()
![]()
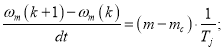
![]()
Электрическая скорость вращения ротора в Simulink-Script (рис. 7):
![]()
![]()
Рис. 7. Математическая модель определения электрической скорости вращения ротора в Simulink-Script
Электрическая скорость вращения ротора в Matlab-Script:
![]()
Реализация математической модели асинхронного двигателя с короткозамкнутым ротором с переменными is – ψr в Matlab-Script в системе относительных единиц приведена в листинге 1.
Листинг 1
% Номинальные данные
PN=320000; UsN=380; IsN=324; fN=50; Omega0N=104.7;
OmegaN=102.83; nN=0.944; cos_phiN=0.92; zp=3;
% Параметры Т-образной схемы замещения при номинальной частоте
Rs=0.0178; Xs=0.118; Rr=0.0194; Xr=0.123; Xm=4.552; J=28;
% Базисные величины системы относительных единиц
Ub=sqrt(2)*UsN;
Ib=sqrt(2)*IsN;
OmegasN=2*pi*fN;
Omegab=OmegasN;
Omegarb=Omegab/zp;
Zb=Ub/Ib;
kd=1.0084;
Mb=kd*PN/OmegaN;
Pb=Mb*Omegarb;
% Расчет коэффициентов
rs=Rs/Zb;
lbs=Xs/Zb;
lbr=Xr/Zb;
lm=Xm/Zb;
Tj=J*Omegarb/Mb;
betaN=(Omega0N-OmegaN)/Omega0N;
SsN=3*UsN*IsN;
ZetaN=SsN/Pb;
kr=lm/(lm+lbr);
lbe=lbs+lbr+lbs*lbr*lm^(-1);
roN=0.9962;
rrk=roN*betaN;
Tr=lm/(rrk*kr);
Tr1=Tr/Omegab;
re=rs+rrk*kr^2;
Te=kr*lbe/re;
Te1=Te/Omegab;
% Расчет модели асинхронного двигателя
K=input('Длительность цикла k=');
for k=1:(K+1)
Um=1; wk=1; dt=0.000001;
Usa=Um*cos(wk*(k-1)*dt);
Usb=Um*cos(wk*(k-1)*dt-2*pi/3);
Usc=Um*cos(wk*(k-1)*dt-4*pi/3);
% 1 ступень прямого преобразования координат a,b,c -> alfa,beta
us_alfa=(1/3)*(2*Usa-Usb-Usc);
us_beta=(1/sqrt(3))*(Usb-Usc);
% 2 ступень прямого преобразования координат alfa,beta -> x,y
teta(1)=0;
teta(k+1)=teta(k)+wk*dt;
rox=cos(teta(k+1));
roy=sin(teta(k+1));
usx(k)=rox*us_alfa+roy*us_beta;
usy(k)=-roy*us_alfa+rox*us_beta;
% Расчет асинхронного двигателя
isx(1)=0; isy(1)=0; psirx(1)=0; psiry(1)=0;
wm(1)=0; w(1)=0; mc=0;
isx(k+1)=isx(k)+(-isx(k)+(1/re)*usx(k)+rrk*(kr^2)/ (re*lm)*psirx(k)+(kr/re)*w(k)*psiry(k)+(kr*lbe/re)*wk*isy(k))*dt/Te1;
isy(k+1)=isy(k)+(-isy(k)+(1/re)*usy(k)+rrk*(kr^2)/(re*lm)*psiry(k)-(kr/re)*w(k)*psirx(k)-(kr*lbe/re)*wk*isx(k))*dt/Te1;
psirx(k+1)=psirx(k)+(-psirx(k)+lm*isx(k)+(lm/(rrk*kr))*(wk-w(k))*psiry(k))*dt/Tr1;
psiry(k+1)=psiry(k)+(-psiry(k)+lm*isy(k)-(lm/(rrk*kr))*(wk-w(k))*psirx(k))*dt/Tr1;
m(k)=ZetaN*kr*(psirx(k+1)*isy(k+1)-psiry(k+1)*isx(k+1));
wm(k+1)=wm(k)+(m(k)-mc)*dt/Tj;
w(k+1)=wm(k+1)*zp;
% mass
mass_t(k)=k*dt;
mass_m(k)=m(k);
mass_w(k)=w(k+1);
end;
% Построение графиков
figure(1);
plot(mass_t,mass_w,'b');
grid on;
figure(2);
plot(mass_t,mass_m,'b');
grid on;
Результаты моделирования асинхронного двигателя в Matlab-Script даны на рис. 8.
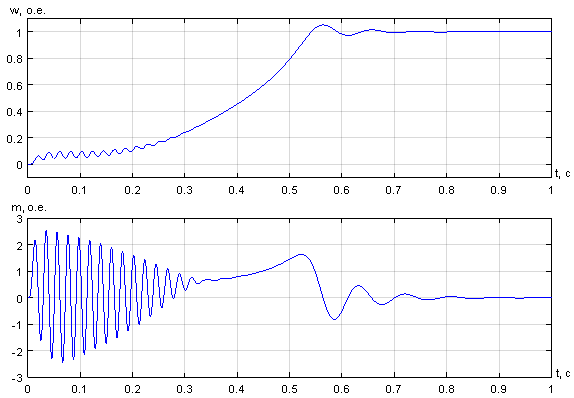
Рис. 8. Графики скорости и электромагнитного момента
Литература:
- Емельянов А.А., Бесклеткин В.В., Иванин А.Ю., Соснин А.С., Воротилкин Е.А., Забузов Е.И., Волков Е.Н., Вандышев Д.М., Власова А.А., Попов С.Ю. Моделирование асинхронного двигателя с переменными is – ψr на выходе апериодических звеньев в Simulink-Script с базовым вариантом // Молодой ученый. - 2017. - №12. - С. 1-10.
- Шрейнер Р.Т. Математическое моделирование электроприводов переменного тока с полупроводниковыми преобразователями частоты. - Екатеринбург: УРО РАН, 2000. - 654 с.
- Шрейнер Р.Т. Электромеханические и тепловые режимы асинхронных двигателей в системах частотного управления: учеб. пособие / Р.Т. Шрейнер, А.В. Костылев, В.К. Кривовяз, С.И. Шилин. Под ред. проф. д.т.н. Р.Т. Шрейнера. - Екатеринбург: ГОУ ВПО «Рос. гос. проф.-пед. ун-т», 2008. - 361 с.