Работа посвящена автоматизации и моделированию решения квазистатических и динамических задач вязкоупругих пластин произвольной конфигурации при различных моделях вязкости в среде системе Maple.
Отметим что, значение вычислительного эксперимента трудно переоценить, особенно, если натурный эксперимент опасен, дорог или просто невозможен. Только разумное сочетание аналитических и численных методов является необходимым условием успеха при решении практических задач.
Как известно, математическая модель данной задачи имеет вид:
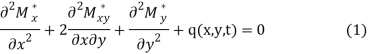
Отметим что, если при формулировке основных физических соотношений используем гипотезу о постоянстве коэффициента Пуассона, тогда изгибающие и крутящие моменты вычисляется следующими формулами:
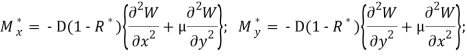
![]()
где D- жесткость вязкоупругих пластин; ![]() интегральный оператор с ядрами релаксации R(t), т. е.
интегральный оператор с ядрами релаксации R(t), т. е. 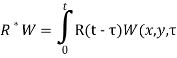 )d
)d![]() — прогиб пластины;
— прогиб пластины;
µ — коэффициент Пуассона; q(x,y,t)-интенсивность внешней нагрузки.
Если же используем гипотеза об упругости объемных деформации, тогда для изгибающих и крутящего моментов вычисляется следующими формулами
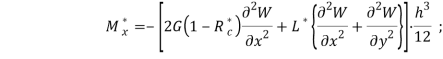
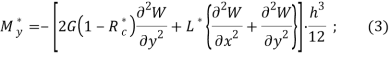
![]()
где G=E/2(1+µ) — модуль сдвига; E — модуль упругости; ![]() — интегральный оператор с ядрами сдвиговой релаксации
— интегральный оператор с ядрами сдвиговой релаксации ![]()
![]() — интегральный оператор, т. е.
— интегральный оператор, т. е.
![]()
K=E/3(1- 2µ) — объемный модуль упругости; h — толщина пластины.
Как известно, уравнение колеблющейся тонкой вязкоупругой плиты имеет вид
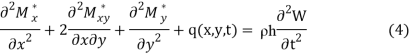
где ρh — масса плиты, отнесенная к единице поверхности.
Уравнения (4) решаются при соответствующих граничных и начальных условиях
![]()
где ![]() — дифференциальные операторы, зависящие от граничных условий; Г — граница области;
— дифференциальные операторы, зависящие от граничных условий; Г — граница области; ![]() и
и ![]() — начальные значения.
— начальные значения.
Решения уравнений (1) и (4) ищем в виде
W(x,y,t)=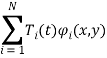 (6)
(6)
где ![]() - системы координатных функций (полиномы Чебышева, степенные, тригонометрические, сплайны Шенберга и т. д.) СКФ.
- системы координатных функций (полиномы Чебышева, степенные, тригонометрические, сплайны Шенберга и т. д.) СКФ.
Отметим что, СКФ точно удовлетворяют всех граничных условий, которые строятся с помощью метода R — функций В. Л. Рвачева [1];
![]() — неизвестные функции времени t.
— неизвестные функции времени t.
Сначала рассмотрим задачи квазистатического изгиба свободно опертых вязкоупругих пластин, изображенных на рисунке 1. Пусть пластина находится под действием нагрузки (q=1). В качестве ядра сдвиговой релаксации используется ядро R(t)=ε.
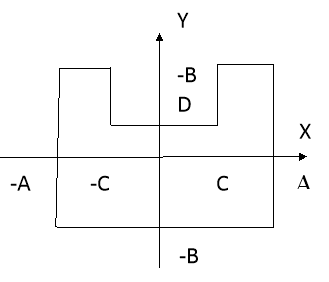
Рис. 1.
С целью численного решения поставленной задачи воспользуемся структурой
W(x,y)= ωΦ1- ω2 /2∙ [Φ1(D2ω+μТ2ω)+2D1Φ1 — ωΦ2] (7)
В приведенных структурных формулах Ф1 и Ф2 –неопределенные компоненты структуры, которые представляется в виде
Фs=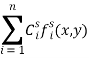 ,
, ![]() - неизвестные компоненты, подлежащие определению,
- неизвестные компоненты, подлежащие определению, ![]() — полная линейно-независимая система функций; D2, T2-дифференциальные операторы R-функций, ω — нормализованная уравнения границы области.
— полная линейно-независимая система функций; D2, T2-дифференциальные операторы R-функций, ω — нормализованная уравнения границы области.
Присутствие двух и более числа неопределенных функций в структуре создает трудности при решении краевых задач. Примем одну из неопределенных функций равной нулю. Например, в (7) положим Ф1 ≠ 0 и Ф2=0, но нельзя Ф2 ≠ 0 и Ф1=0, так как это обстоятельство приводит к появлению «лишнего» граничного условия [1].
Нормализованное уравнение геометрии области для пластины, представленной на рис.1, имеет вид:
Ω=((Ω 1 ![]() (-Ω 2)) (8)
(-Ω 2)) (8)
где Ω 1 =(a2-x2)/2a ![]() (b2-y2)/2b, Ω 2 =(c2-x2)/2c
(b2-y2)/2b, Ω 2 =(c2-x2)/2c ![]() (y-d)
(y-d)
![]() — оператор логический конъюнкции нулевого порядка.
— оператор логический конъюнкции нулевого порядка.
Отметим что, при решение краевых задач используется ортонормированное СКФ по бигармоническому и единичному оператору соответственно и далее для решения автономным систем интегральных и интегро-дифференциальных уравнений применяется численный метод, основанный на использовании квадратурных формул [2].
На рис.2, а показано изменение прогиба W(x,y,t) во времени (пунктирная линия) по оси ОХ и y=0.2, а на рис.2,б — изменение изгибающего ![]() и крутящего
и крутящего ![]() моментов (пунктирная линия) в той же точке. Cсплошными линиями показано изменение тех же величин для пластины с постоянными во времени коэффициентом Пуассона и ядром релаксации, совпадающим с ядром Rc(t) для рассматриваемой пластины.
моментов (пунктирная линия) в той же точке. Cсплошными линиями показано изменение тех же величин для пластины с постоянными во времени коэффициентом Пуассона и ядром релаксации, совпадающим с ядром Rc(t) для рассматриваемой пластины.
Отметим что, когда используется гипотеза о постоянстве коэффициента Пуассона, тогда прогиб не изменяется во времени t.
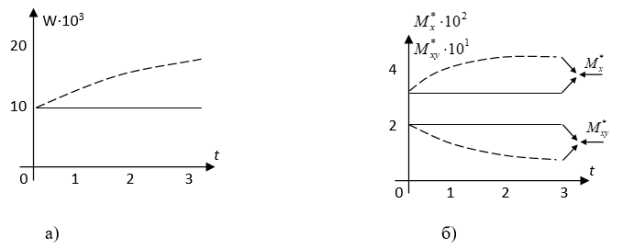
Рис. 2.
Результаты получены при следующих значениях безразмерных параметров:
Λ=a/b=1; c/a=0.5; d/a=0.2; ε=0.05; β=0.075; µ=0.17
Здесь мы сравнивали полученные результаты на основе двух гипотезы. Численное результаты показывает что, результаты полученные на основе гипотеза об упругости объемных деформации хорошо согласуется с результатами эксперимента,
Далее рассмотрим вынужденные колебания жестко защемленных вязкоупругих пластин (рис.1). Пусть пластина находится под действием нагрузки (q=1) и при следующих начальных условиях W|t=0=0, Wt|t=0=0.
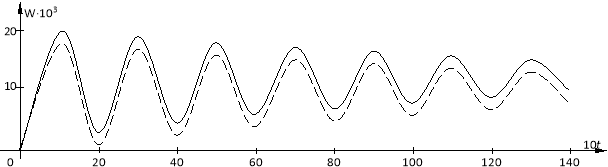
Рис. 3.
Результаты получены при следующих значениях безразмерных параметров:
Λ=a/b=1; c/a=0.5; d/a=0.2; ε=0.05; β=0.075; µ=0.17
На рис.3 показано изменение прогиба пластины W(0.0;0.2;t) полученные на основе двух гипотезы. Для сравнения сплошными линиями показано изменение прогиба пластины W(0.0;0.2;t), полученное на основе гипотезы о постоянстве коэффициента Пуассона.
В табл.1 для c/a=0.5; d/a=0.5 приведены значения частотного параметра λi первых трех тонов колебаний упругих пластин, полученные с помощью степенного полинома. Соответствующие значения частотного параметра wi определяется по формуле wi=λi/a2√D/ρh. Здесь для определения собственных чисел λi применяется QL — метод.
Количество СКФ варьировалось от 15 до 36, при этом наблюдалась хорошая сходимость чисел λi.
Таблица 1
|
λi |
N=15 |
N=21 |
N=28 |
N=36 |
|
λ1 |
10.115 |
8.562 |
8.265 |
7.922 |
|
λ2 |
19.272 |
18.013 |
16.284 |
16.127 |
|
λ3 |
27.822 |
26.717 |
22.312. |
21.531 |
Метод R-функции позволяет построить координатные последовательности для областей практически произвольной конфигурации и краевых условий сложного вида. Построен эффективный вычислительный алгоритм для расчета задач наследственной теории вязкоупругости со сложной формой границы на основе комбинации методов R-функции и вариационных методов [3]. На основе предложенного вычислительного алгоритма разработано интеллектуальной алгоритмической системы.
С помощью разрабонной интеллектуальной алгоритмической системы можно решать целый класс задач механики деформируемого твердого тела и легко его обобщить для других задач математической физики.
Литература:
- Рвачев В. Л., Курпа Л. В. R-функций в задачах теории пластин. Киев: Наукова думка.1987.176 с.
- Бадалов Ф. Б. Методы решения интегральных и интегро-дифференциальных уравнений наследственной теории вязкоупругости. Ташкент. Мехнат.1987.289 с.
- Назиров Ш. А., Садиков Х. С. Комплекс программных средств для решения краевых задач вариационными методами./Алгоритмы. Ташкент: РИСО АН Уз.Вып.65.1988.

