Библиографическое описание:
Давронов, Ж. Р. Экстремальная функция и представление нормы функционала погрешности / Ж. Р. Давронов. — Текст : непосредственный // Молодой ученый. — 2017. — № 25 (159). — С. 4-6. — URL: https://moluch.ru/archive/159/44896/ (дата обращения: 19.04.2024).
Функция 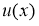 из
из 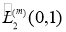 называется экстремальной функцией для функционала погрешности
называется экстремальной функцией для функционала погрешности 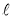 , если выполняется равенство
, если выполняется равенство
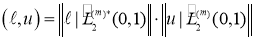 .
.
Пространство 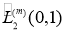 является гильбертовым и скалярное произведение в этом пространстве дается формулой
является гильбертовым и скалярное произведение в этом пространстве дается формулой 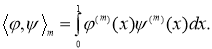
По теореме Рисса любой линейно непрерывный функционал 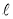 в гильбертовом пространстве представляется в виде скалярного произведения
в гильбертовом пространстве представляется в виде скалярного произведения
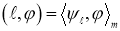 (1)
(1)
для любой функции из 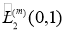 . Здесь
. Здесь 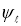 — функция из пространства
— функция из пространства 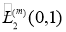 , определяется единственным образом по функционалу
, определяется единственным образом по функционалу 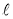 и является его экстремальной функцией. Интегрируя по частям выражения в правой части равенства (1) и используя периодичность функций
и является его экстремальной функцией. Интегрируя по частям выражения в правой части равенства (1) и используя периодичность функций 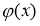 и
и 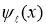 , получаем равенство
, получаем равенство
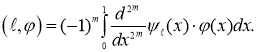
Таким образом, экстремальная функция 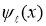 является обобщенным решением уравнения
является обобщенным решением уравнения
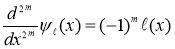 (2)
(2)
с граничными условиями
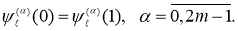
Для экстремальной функции имеет место следующая
Теорема 1.1. Явное выражение для экстремальной функции 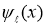 функционала погрешности
функционала погрешности 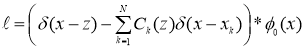
определяется формулой
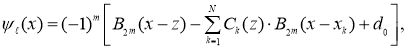 (3)
(3)
где 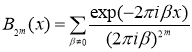 является полиномом Бернулли,
является полиномом Бернулли, 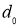 – константа.
– константа.
Доказательство. Используем формулы преобразования Фурье, данный в [1], cвертка двух функций определяется формулой
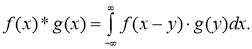
Применяя к обеим частям равенства (2) преобразование Фурье и используя известные формулы (см. [17])
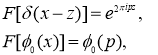
получаем
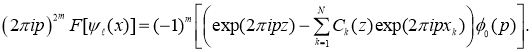
(4)
В силу (4) правая часть равенства (4) равна нулю в начале координат. Следовательно, обе части уравнения (4) делятся на 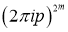 .
.
Функция 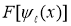 определяется из (4) до выражения
определяется из (4) до выражения
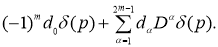
Но, как известно, периодическое решение однородного уравнения, соответствующего уравнению (2), является константой, тогда все члены, кроме 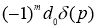 до последнего выражения, должны быть отброшены. Таким образом, из (4) имеем
до последнего выражения, должны быть отброшены. Таким образом, из (4) имеем
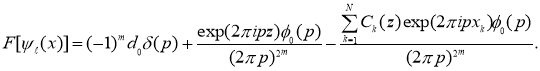
Отсюда, с учетом
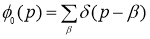 и
и 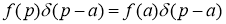
имеем
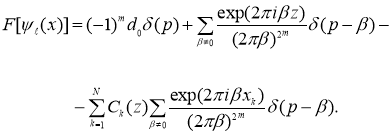
Применяя к обеим частям последнего равенства обратное преобразование Фурье, получаем
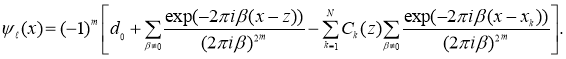
Отсюда, используя определение полинома Бернулли
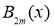
, получим (3)
Литература:
-
Соболев С. Л. Введение в теорию кубатурных формул. -М.: Наука, 1974.
-
Шадиметов Х. М. Дискретный аналог дифференциального оператора
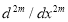 и его построение// Вопросы вычислительной и прикладной математики: Сб. науч. тр. Ташкент, ИК АН Узбекистана, -вып. 79, 1985. –С. 22–35. arXiv:1001.0556 [NA.math].
и его построение// Вопросы вычислительной и прикладной математики: Сб. науч. тр. Ташкент, ИК АН Узбекистана, -вып. 79, 1985. –С. 22–35. arXiv:1001.0556 [NA.math].
-
Шадиметов Х. М. Оптимальные решетчатые квадратурные и кубатурные формулы в пространствах Соболева. Дис. докт. физ.-мат. наук. -Ташкент, 2002. -218 с.
Основные термины (генерируются автоматически): экстремальная функция, правая часть равенства, скалярное произведение, функция.
Похожие статьи
— скалярное произведение в , определенное равенством и согласованное с нормой в ; — билинейная форма, заданная на , , ; — шар в радиуса с центром в нуле; — носитель суммируемой функции
Умножая скалярно обе части последнего равенства на и меняя затем в правой части порядок интегрирования, получим. Переходя здесь к пределу при и , получим соотношение. . Теорема доказана для любой вектор функции из пространства...
Если значения интеграла (4) принять за скалярное произведение векторных функций и , то превратится в гильбертово пространство, в общем случае — неполное.
Интегрируя почленно левую и правую части формулы Лагранжа (6), получим формулу Грина.
Скачать Часть 1 (pdf). Библиографическое описание
, . Здесь и вещественнозначные непрерывные функции на .
, их скалярное произведение определяется по равенству: , где.
со скалярным произведением.
Задача 2.Найти такие значения и , чтобы выполнялось равенство (5).
Теорема 2.Функция. является экстремальной функцией для кубатурной формулы (1) и .
Скачать Часть 1 (pdf). Библиографическое описание
Пусть имеется евклидово пространство, элементами которого являются функции аргумента , со скалярным произведением .
Экстремальная функция и представление нормы функционала погрешности. Обсуждение.
Скачать Часть 1 (pdf). Библиографическое описание
Сначала дадим определение квадратичного числового образа оператора и некоторые информации о нем (для подробности смотрите работу [5]). Пусть и -скалярное произведение и норма в , соответственно.
Скачать Часть 1 (pdf). Библиографическое описание
, то их скалярное произведение определяется по равенству
Если рассмотрим симметричные функции [2], то получается стандартное бозонное пространства Фока, в случае антисимметричных функций получается...
в гильбертовом пространстве вектор-функций , рассматриваемых как вектор-столбцы, со скалярным произведением.
Об одной задаче определения правой части линейного дифференциального уравнения четвертого порядка.
— скалярное произведение в , определенное равенством и согласованное с нормой в ; — билинейная форма, заданная на , , ; — шар в радиуса с центром в нуле; — носитель суммируемой функции
Умножая скалярно обе части последнего равенства на и меняя затем в правой части порядок интегрирования, получим. Переходя здесь к пределу при и , получим соотношение. . Теорема доказана для любой вектор функции из пространства...
Если значения интеграла (4) принять за скалярное произведение векторных функций и , то превратится в гильбертово пространство, в общем случае — неполное.
Интегрируя почленно левую и правую части формулы Лагранжа (6), получим формулу Грина.
Скачать Часть 1 (pdf). Библиографическое описание
, . Здесь и вещественнозначные непрерывные функции на .
, их скалярное произведение определяется по равенству: , где.
со скалярным произведением.
Задача 2.Найти такие значения и , чтобы выполнялось равенство (5).
Теорема 2.Функция. является экстремальной функцией для кубатурной формулы (1) и .
Скачать Часть 1 (pdf). Библиографическое описание
Пусть имеется евклидово пространство, элементами которого являются функции аргумента , со скалярным произведением .
Экстремальная функция и представление нормы функционала погрешности. Обсуждение.
Скачать Часть 1 (pdf). Библиографическое описание
Сначала дадим определение квадратичного числового образа оператора и некоторые информации о нем (для подробности смотрите работу [5]). Пусть и -скалярное произведение и норма в , соответственно.
Скачать Часть 1 (pdf). Библиографическое описание
, то их скалярное произведение определяется по равенству
Если рассмотрим симметричные функции [2], то получается стандартное бозонное пространства Фока, в случае антисимметричных функций получается...
в гильбертовом пространстве вектор-функций , рассматриваемых как вектор-столбцы, со скалярным произведением.
Об одной задаче определения правой части линейного дифференциального уравнения четвертого порядка.
![]() из
из ![]() называется экстремальной функцией для функционала погрешности
называется экстремальной функцией для функционала погрешности ![]() , если выполняется равенство
, если выполняется равенство
![]() .
.
![]() является гильбертовым и скалярное произведение в этом пространстве дается формулой
является гильбертовым и скалярное произведение в этом пространстве дается формулой ![]()
![]() в гильбертовом пространстве представляется в виде скалярного произведения
в гильбертовом пространстве представляется в виде скалярного произведения
![]() (1)
(1)
![]() . Здесь
. Здесь ![]() — функция из пространства
— функция из пространства ![]() , определяется единственным образом по функционалу
, определяется единственным образом по функционалу ![]() и является его экстремальной функцией. Интегрируя по частям выражения в правой части равенства (1) и используя периодичность функций
и является его экстремальной функцией. Интегрируя по частям выражения в правой части равенства (1) и используя периодичность функций ![]() и
и ![]() , получаем равенство
, получаем равенство
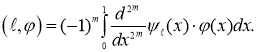
![]() является обобщенным решением уравнения
является обобщенным решением уравнения
![]() (2)
(2)
![]() функционала погрешности
функционала погрешности ![]()
![]() (3)
(3)
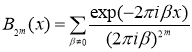 является полиномом Бернулли,
является полиномом Бернулли, ![]() – константа.
– константа.
![]()
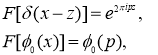
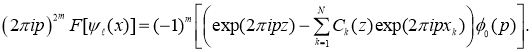 (4)
(4)
![]() .
.
![]() определяется из (4) до выражения
определяется из (4) до выражения
![]()
![]() до последнего выражения, должны быть отброшены. Таким образом, из (4) имеем
до последнего выражения, должны быть отброшены. Таким образом, из (4) имеем
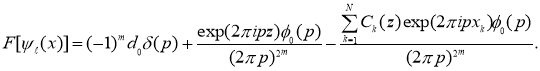
![]() и
и ![]()
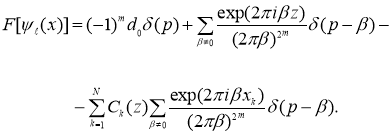
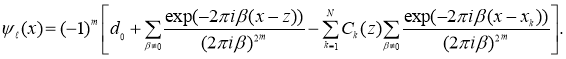 Отсюда, используя определение полинома Бернулли
Отсюда, используя определение полинома Бернулли 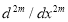 и его построение// Вопросы вычислительной и прикладной математики: Сб. науч. тр. Ташкент, ИК АН Узбекистана, -вып. 79, 1985. –С. 22–35. arXiv:1001.0556 [NA.math].
и его построение// Вопросы вычислительной и прикладной математики: Сб. науч. тр. Ташкент, ИК АН Узбекистана, -вып. 79, 1985. –С. 22–35. arXiv:1001.0556 [NA.math].







