Саморегуляция учебной деятельности — это специфическая регуляция, осуществляемая обучающимся как субъектом деятельности. В результате обучающийся осознаёт свои задачи в качестве субъекта учебной деятельности, целенаправленно строит процесс самообучения. Исследователи саморегуляции учебной деятельности отмечают, что её структура такова же, как у других видов деятельности.
В структуре саморегуляции О. А. Конопкин [1] выделяет следующие функциональные звенья: цель деятельности, субъективная модель значимых условий, программа исполнительских действий, система субъективных критериев достижения цели, контроль и оценка реальных результатов, решение о коррекции системы.
Принимая эту концепцию, В. И. Моросанова [2] исследует операциональный аспект процессов саморегуляции учебной деятельности и заключает, что каждое из звеньев реализуется соответствующим регуляторным процессом: планирования целей, моделированием условий, программированием, контролем и коррекцией результатов.
Рассмотрим на примере решения задачи работу каждого функционального звена саморегуляции.
Задача. В прямоугольном треугольнике один из катетов равен 14, а биссектриса прямого угла имеет длину ![]() . Найти стороны данного треугольника.
. Найти стороны данного треугольника.
Анализируем условие задачи, вводим чертёж (рис. 1).
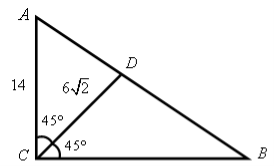
Рис. 1.
Замечаем, что треугольник ACD определён двумя сторонами AC и CD и углом между ними. Применяя теорему косинусов, находим ![]() .
.
Дальнейший анализ условия показывает, что для нахождения сторон треугольника достаточно определить длины BC и BD.
Планируемая цель: найти соотношения, которыми связаны длины BC и BD и известные величины треугольника.
Моделирование условий, имеющихся в задаче, можно осуществить, отвечая на вопросы, предлагаемые учителем. Какие связи для сторон треугольников известны в математике? Какими свойствами обладает биссектриса треугольника? Сколько неизвестных величин? Сколько уравнений связи необходимо написать?
В модель значимых условий вводим известные соотношения между сторонами треугольника (теорема Пифагора, теорема косинусов) и свойство биссектрисы.
Составляем программу исполнительских действий:
-
Ввести удобные обозначения:
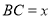 и
и 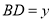 (рис. 2).
(рис. 2).
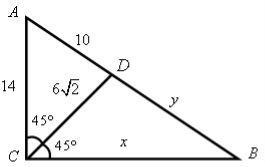
Рис. 2.
-
Составить систему уравнений
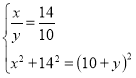
- Решить систему.
Планируется новая цель деятельности — решить систему уравнений.
Моделируем условия, отбираем значимые. Какие уравнения в системе? Какие есть методы решения систем уравнений? Есть ли в системе линейное уравнение? Можно ли применить метод подстановки? Какую переменную удобней выразить из первого уравнения? В каких дробях удобней работать — десятичных или обыкновенных?
В модель значимых условий вводим метод подстановки для решения систем уравнений, рациональные способы решения систем уравнений, рациональные способы счёта.
Составляем программу исполнительских действий:
- Выражаем х из первого уравнения и подставляем во второе.
- Решаем квадратное уравнение.
- Находим x, зная y.
В результате вычислений получаем две пары чисел ![]() и
и ![]() .
.
- Вычисляем стороны треугольника.
После того как вычисления закончены, учитель задаёт вопрос, решена ли задача. Достигнута ли цель — решить задачу?
Система субъективных критериев достижения цели предполагает обратиться к первоначальному тексту задачи. Решение не закончено. Необходимо сделать контроль. Анализируя текст задачи на определённость геометрической конфигурации, замечаем, что треугольник ACD единственный, и положение точки B однозначно определено. Делаем вывод, что задача имеет единственное решение, а, значит, в приведённом решении имеется ошибка.
Делаем вывод о необходимости коррекции полученных результатов. Проверке подвергается: общий план решения, затем отдельно каждый этап. Единственный этап, который вызывает сомнения после проверки — это этап перевода задачи с геометрического языка представления информации на алгебраический язык.
Планируется новаяцель: проверить эквивалентность построенной модели. Если x и y длины указанных на чертеже отрезков, то они точно удовлетворяют каждому уравнению полученной системы. В процессе решения системы равносильность нарушена не была. Надо проверить, будет ли каждое решение системы удовлетворять условию задачи. Рекомендуется восстановить чертёж по системе уравнений (рис. 3).
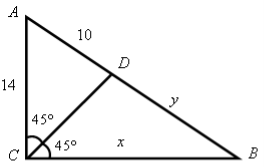
Рис. 3.
Как видим, точка D остаётся основанием биссектрисы, но её длина не известна (допускает два значения на основании теоремы косинусов для треугольника ACD).
В результате моделирования значимых условий, приходим к выводу о приобретении постороннего решения. А, значит, цель не достигнута: стороны треугольника не найдены. Необходимо отделить истинное решение задачи от постороннего. Планируется новая цель: проверить, какие из найденных отрезков, удовлетворяют условию задачи.
В модель значимых условий вводим способы проверки, другие способы решения задачи, вычисление биссектрисы CD при найденных значениях x, y.
Составляем программу исполнительских действий:
- Вычислить CD при найденных значенияхx, y.
-
Отобрать те x, y, при которых
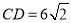 .
.
При 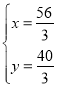 получаем
получаем ![]() или
или ![]() .
.
При
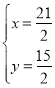 получаем
получаем Получаем стороны треугольника: 14; 10,5; 17,5.
Возвращаемся к Системе субъективных критериев достижения цели и делаем вывод, что такой треугольник удовлетворяет условию задачи.
Завершаем решение задачи оценкой реальных результатов. На этом этапе анализируется каждый шаг с целью проверки выполненных логических следствий и поиска нового метода решения; выделяются все основные математические знания, способы и методы решения задачи; выделяются те знания, способы и приёмы, которые обучающийся впервые познал в процессе решения задачи.
Для этой задаче можно предложить ещё такие способы решения (рис. 4).
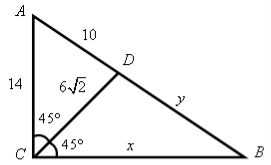
Рис. 4.
- Оставить уравнение, основанное на свойстве биссектрисы, второе уравнение — теорема косинусов для стороны BDтреугольника BCD:
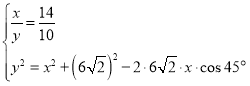
В этом случае также происходит захват постороннего решения ![]() . (В этом случае
. (В этом случае ![]() ). Из системы не следует, что точки A, B, D лежат на одной прямой.
). Из системы не следует, что точки A, B, D лежат на одной прямой.
- Систему составить на основании теоремы косинусов для треугольника BCD и теоремы Пифагора для треугольника ABC.
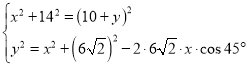
В этом случае захвата постороннего решения не происходит. (CD получается биссектрисой, и точки A, B, D лежат на одной прямой).
- Заметим ещё, что если первый способ дополнить, к примеру, теоремой косинусов для треугольника BCD, а второй — теоремой Пифагора, то также не будет захвата посторонних решений.
С точки зрения М. А. Холодной, средствами, необходимыми ученику для реализации регуляторного процесса при усвоении учебной информации, являются интеллектуальные умения, связанные со спецификой учебного предмета [3]. В когнитивной психологии установлено, что развитый интеллект человека характеризуют способности: к моделированию, к индуктивному и дедуктивному рассуждениям, к пониманию. Развитие этих способностей в значительной степени происходит при обучении математике.
Приведённый пример показывает, что саморегуляция деятельности по решению задачи выполняется непрерывно, и обеспечивает, с одной стороны, овладение учеником математическими знаниями, а с другой — способом приобретения этих знаний. Как показывает опыт, обнаружение ошибки на этапе моделирования, анализ причин, приводящих к появлению посторонних решений и коррекция — важные новые знания учащихся.
Литература:
- Конопкин О. А. Психическая саморегуляция произвольной активности человека (структурно-функциональный аспект) [Электронный ресурс]. — Режим доступа: http://www.eduhmao.ru/info/1/3952/25078/
- Моросанова В. И. Индивидуальный стиль саморегуляции произвольной активности человека: Автореф. дис. доктора психологических наук. Москва, 1995. — 38 c.
- Холодная М. А. Психология интеллекта: парадоксы исследования / М. А. Холодная. — Томск: Изд-во Том. ун-та; М.: Барс. 1997. — 392 с.







