Новые обобщения определения параболы
Целью работы является обобщение определения параболы в том случае, когда фокус превращается в фокальную окружность.
Парабола — геометрическое место точек, равноудалённых от данной прямой (называемой директрисой параболы) и данной точки (называемой фокусом параболы) [1, c.85].
Каноническое уравнение параболы в прямоугольной системе координат: 
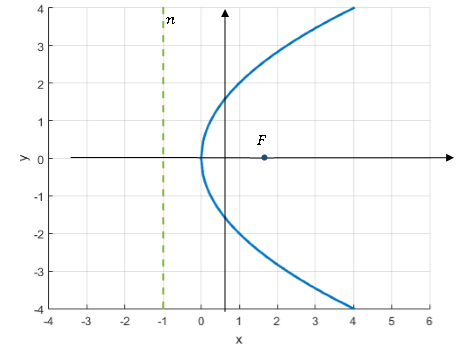
Рис. 1. Парабола
Директриса — прямая 
, лежащая в плоскости конического сечения и обладающая тем свойством, что отношение расстояния от любой точки кривой до фокуса 
кривой к расстоянию от той же точки до этой прямой есть величина постоянная, равная эксцентриситету.
Эксцентриситет — числовая характеристика конического сечения, показывающая степень его отклонения от окружности. Для параболы эксцентриситет равен 
.
В данной работе исследуется случай, при котором вместо фокуса-точки рассматривается фокальная окружность радиуса 
, центр которой находится в начале системы координат.
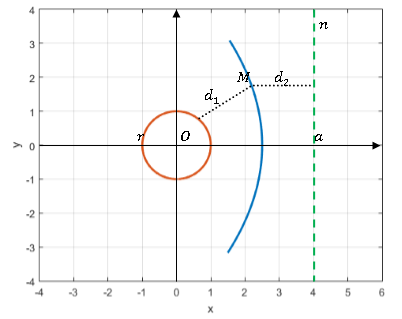
Рис. 2. Фокальная окружность
Найдем 
, если точка 
расположена вне круга:
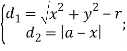
тогда уравнение геометрического места точек:
(1)
Если же точка расположена внутри круга, то:
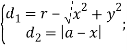
(2)
Для описания данного геометрического места точек необходимо отдельно рассмотреть следующие случаи:
-
Точка
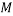находится вне окружности (и на ее границе):
-
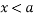— Рассматривается участок слева от директрисы.
-
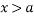— Рассматривается участок справа от директрисы.
-
.
-
-
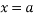Точка 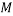находится внутри окружности:
-
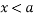— Рассматривается участок слева от директрисы.
-
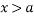— Рассматривается участок справа от директрисы.
-
.
-
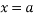Рассмотрим все случаи 
для уравнения (1). Перенесем в правую часть и избавимся от радикала, возведя обе части в квадрат:
раскроем модуль для случая 1.a:
Сгруппировав слагаемые и вынеся общие множители, получим следующее уравнение:
которое можно привести к виду 
Однако для построения графиков удобнее будет воспользоваться следующим видом:
Очевидно, что обязательно подкоренное выражение не должно быть отрицательным. Рассмотрим данное неравенство подробнее.
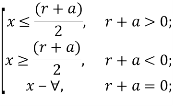
Таким образом, необходимо учитывать ряд ограничений на область определения:
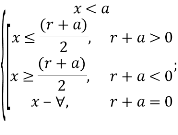
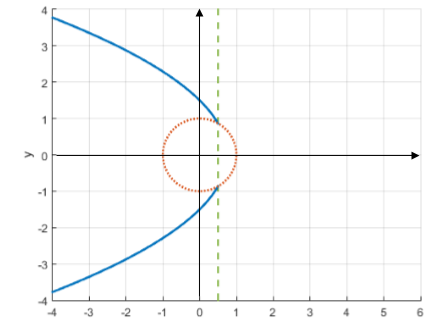
Рис. 3. ГМТ 1.а при 
Рассматривая аналогичным образом случаи 1.b и 1.c, получим:
Для 1.b:
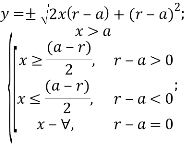
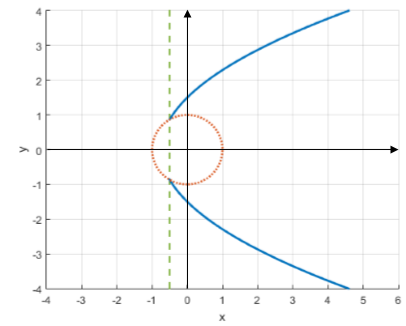
Рис. 4. ГМТ 1.b при 
Для 1.c:
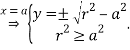
Перейдем теперь к рассмотрению случая 2. Так как расстояние от любой точки внутри окружности до ее границы не может превосходить радиус этой окружности 
то логично потребовать этого же и от расстояния до прямой: 
. Что, в свою очередь, даст условие 
. В (2) подставим условия случая 2.а:
перенесем в правую часть и избавимся от радикала, возведя обе части в квадрат:
возведя обе части равенства в квадрат, получим:
Также на область определения накладывается условие расположения внутри окружности: 
, где 
определяется соответствующим рассматриваемому случаю уравнением ГМТ. Для случая 2.а:
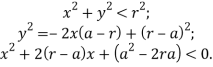
Старший коэффициент параболы больше нуля, следовательно, допустимая область находится между корнями уравнения. Решим данное квадратное уравнение:
Таким образом, в случае 2.а:
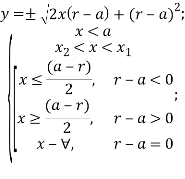
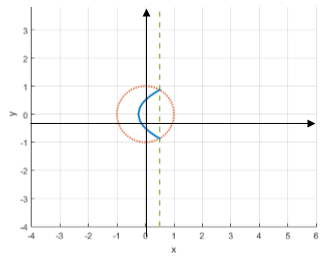
Рис. 5. ГМТ 2.а при
Перейдем к случаю 2.b. Аналогично с 2.а, получим ГМТ:
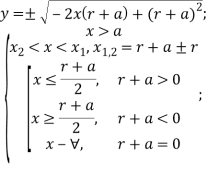
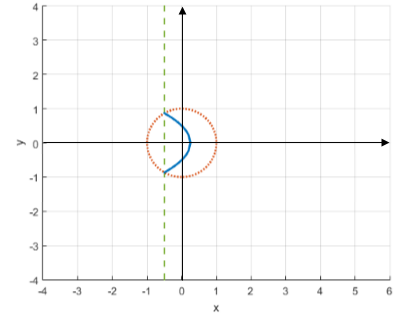
Рис. 6. ГМТ 2.b при
В целом, случай 2.с аналогичен случаю 1.с:
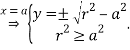
Можно сделать вывод, что при 
, будет наблюдаться следующая картина:
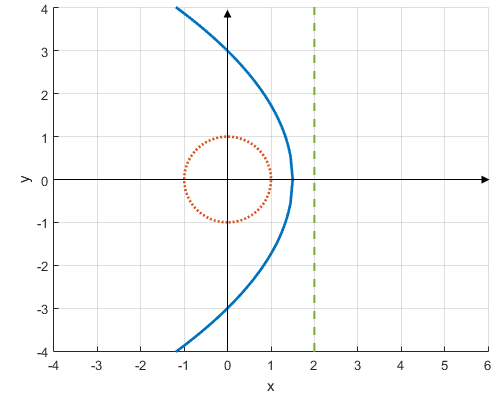
Рис. 7. Авторская парабола при 
Иначе, при 
:
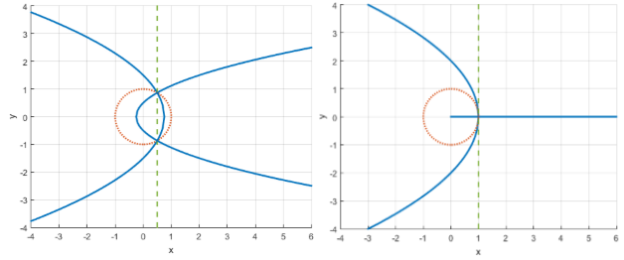
Рис. 8. Авторская парабола при 
В результате исследования найдены возможные обобщения параболы в случае, когда фокус превращается в фокальную окружность. Эти обобщения представлены на рисунках 6–8.
Литература:
- Д. В. Клетеник «Аналитическая геометрия»
