Рассмотрим интегро-дифференциальное уравнение с малым параметром.
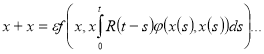 (1)
(1)
где ![]() малый параметр
малый параметр ![]()
![]() некоторая непрырывная функция своих аргументов.
некоторая непрырывная функция своих аргументов. 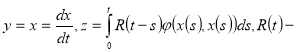 ядро
ядро
Согласно методу двух масштабного разложения ишем решение уровнение (1) в виде асимптотического ряда [1,2]
![]() (2)
(2)
где ![]() (3)
(3)
Постоянные ![]() определяем из условия ограниченности решений
определяем из условия ограниченности решений
Поставляя значения ![]() и
и ![]() определяемые равенствами (3) в правую часть разложения (2) находим
определяемые равенствами (3) в правую часть разложения (2) находим
![]() (4)
(4)
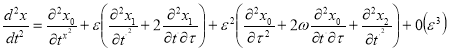 (5)
(5)
Далее разлогая функцию ![]() в ряд по степеням
в ряд по степеням ![]() имеем
имеем
![]()
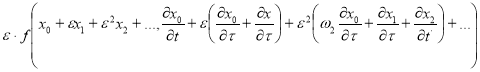
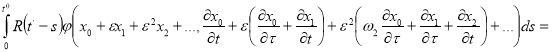
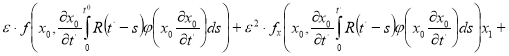
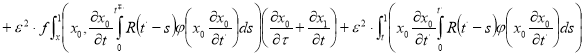
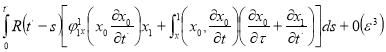 (6)
(6)
![]() Поставляя соотношения (2), (5), и (6) в уравнение (1) и приравнивая коэффициенты пари одинаковых степеней фф получаем
Поставляя соотношения (2), (5), и (6) в уравнение (1) и приравнивая коэффициенты пари одинаковых степеней фф получаем
![]() (7)
(7)
![]()
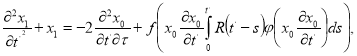 (8)
(8)
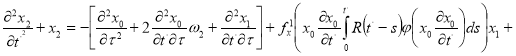
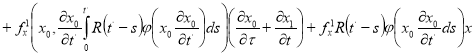
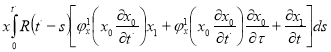 (9)
(9)
Вводя медленно меняющиеся амплитуду ![]() и фазу
и фазу ![]() из уравнения (7) находим
из уравнения (7) находим
![]() (10)
(10)
Поставляя выражение 10 в правую часть уравнения (8) имеем
![]()
![]() (11)
(11)
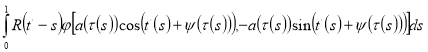
Чтобы исключить появление пекулярных (вековых) членов разложения, необходимо положить [3]
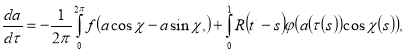
—![]()
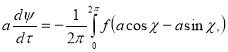
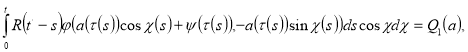 (12)
(12)
где ![]() .
.
Так как ![]() те переходя в уравнении (II) к переменной
те переходя в уравнении (II) к переменной![]() , получаем
, получаем
![]()
(13)
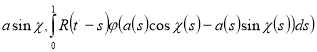
![]() Определим функции
Определим функции ![]() и
и ![]() посредством соотношений.
посредством соотношений.
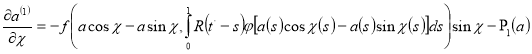
(15)
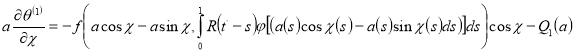
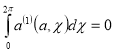
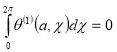
Тогда из уравнения (13) методом вариации параметров, находим
![]() (17)
(17)
где ![]() — медленно меняющиеся функции, определяемые из условия отсутствуют вековых членов в выражениях для
— медленно меняющиеся функции, определяемые из условия отсутствуют вековых членов в выражениях для ![]() .
.
Подставляя равенства (10) и (17) в правую часть уравнения (9) и используя условия отсутствие сингулярных членов в разложений, находим для определения ![]() и
и ![]() уравнения в виде [3, 4]
уравнения в виде [3, 4]
![]() (18)
(18)
![]() ,
,
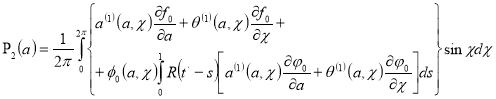 ,
,
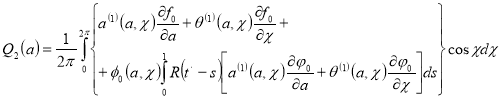 ,
,
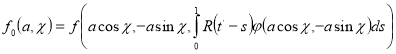
![]()
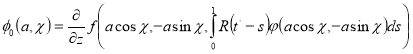
Из системы уравнений (18) следует, что если ![]() , то необходимо положить
, то необходимо положить ![]() так как в противном случае разложение имело бы сингулярные члены. Предположив, что
так как в противном случае разложение имело бы сингулярные члены. Предположив, что ![]() ,из системы (18) найдем медленно меняющиеся функции
,из системы (18) найдем медленно меняющиеся функции ![]() и
и ![]() .
.
Таким образом, определяются остальные последующие члены разложение (2) Следовательно, при вычислении члена ![]() нужно учитывать вид решения
нужно учитывать вид решения ![]() а также равномерную пригодность
а также равномерную пригодность ![]() и
и ![]() на достаточно большом промежутке времени. Итак используя соотношения (2), (4) формуле (10) и выражение (17) имеем
на достаточно большом промежутке времени. Итак используя соотношения (2), (4) формуле (10) и выражение (17) имеем
![]()
Литература:
- Самойленко А. М. «К вопросу обоснования метода усреднения для многочастотных колебательных систем»// Дифференциальные уравнения.1987.№ 23 стр. 276–278
- Бигун Я. Н., Форчук В. И. «применение метода усреднения для исследования одного класса многочастотного систем с запаздыванием» // Укр. Мат. Журнал 1980 № 2 стр. 149–164.
- Филатов А. Н. «Асимптотические методы в теории дифференциальных и интегро-дифференциальных уравнений». Ташкент Фан, АН УзССР, 1974 г.
- Кадырбеков Т. К. «Нелинейные колебания вязкоупругой балки. Механика полимеров». Рига.1973г.

