Блочно-операторные матрицы — это матрицы, элементы которых являются линейными операторами, определенными между банаховым или гильбертовым пространством. Такие операторы возникают в статистической физике, теории твердого тела, теории химических реакции, магнито-гидродинамике, квантовой механике и т. д. Недавно в монографии [1] подробно изучены абстрактные свойства ограниченных и неограниченных блочно-операторных матриц и их применения в некоторых задачах математической физики.
В настоящей работе рассматривается блочно операторная матрица 
, действующая в так называемом двухчастичном обрезанном подпространстве Фоковского пространства. Изучен нули определителя Фредгольма соответствующей оператору 
.
Отметим, что оператор 
можно рассмотреть как одномерное возмущение оператора 
, рассмотренного в работах [2, 3], где изучены пороговые явления для оператора 
.
Пусть 
— компактное связанное множество, 
- гильбертово пространство квадратично интегрируемых (комплекснозначных) функций, определенных на 
и 
— одномерное комплексное пространство.
Обозначим
Гильбертово пространство 
называется двухчастичным обрезанным подпространством Фоковского пространства.
Рассмотрим блочно-операторную матрицу действующую в гильбертовом пространстве и задающуюся как
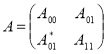, (1)
где матричные элементы 
определяются по формулам
Здесь 
— фиксированное вещественное число, 
— вещественнозначные непрерывные (ненулевые) функции на 
. Здесь и в дальнейшем интеграл без указания пределов всюду означает интегрирование по всей области изменения переменных интегрирования.
В современной математической физике оператор 
называется оператором уничтожения, а оператор 
называется оператором рождения, см. [4].
Легко можно проверить, что оператор , определенный операторной матрицей (1) и действующий в гильбертовом пространстве , является ограниченным и самосопряженным.
Обозначим через 
и 
, соответственно, существенный спектр и дискретный спектр ограниченного самосопряженного оператора.
Пусть оператор действует в как
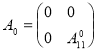
Оператор возмущения 
оператора является ограниченным самосопряженным оператором ранга не более чем 3. Следовательно, из известной теоремы Г. Вейля о сохранении существенного спектра при возмущениях конечного ранга вытекает, что существенный спектр оператора совпадает с существенным спектром оператора . Известно, что
где числа 
и 
определяются равенствами
Из последних двух фактов следует, что
Далее, для формулировки результата работы вводим операторы
и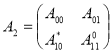 
.
Из определения операторов 
видно, что они имеют более простую структуру чем .
Определим регулярные в 
функции (определитель Фредгольма, ассоциированный с оператором 
соответственно)
.
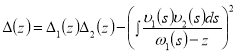Теперь установим связь между собственными значениями оператора и нулями функции 
Верна следующая
Теорема 1. Число 
является собственным значением оператора тогда и только тогда, когда 
.
Теорема 2.Число
является собственным значением оператора 
тогда и только тогда, когда 
.
Литература:
- C. Tretter. Spectral Theory of Block Operator Matrices and Applications. ImperialCollegePress, 2008.
- Т. Х. Расулов. О существовании виртуального уровня обобщенной модели Фридрихса. Узб. Матем. Журнал. 2007, № 4, стр. 56–63.
- Т. Х. Расулов. О собственных значениях обобщенной модели Фридрихса. Узбекский математический журнал, 2006, № 4, стр. 61–68.
- К. О. Фридрихс. Возмущения спектра операторов в гильбертовом пространстве. М.: Мир, 1972.
