Нелинейные колебания резиновой мембраны



Нелинейные колебания резиновой мембраны

Мальцева Любовь Сергеевна, аспирант;

Колпак Евгений Петрович, доктор физико-математических наук, профессор

Санкт-Петербургский государственный университет

Иванов Сергей Евгеньевич, кандидат физико-математических наук, доцент

Санкт-Петербургский национальный исследовательский университет информационных технологий, механики и оптики

Решается динамическая задача о растяжении нормальным давлением мембраны из резино-подобного материала. Исследуется статическое решение. Строится решение для малых колебаний около статического положения равновесия. Решение нелинейных динамических уравнений строится с применением метода сеток.

Ключевые слова: эластомеры, экспериментальные данные, мембрана, деформации, напряжения, упругий потенциал.

Оболочки используются при решении многих задач строительства и машиностроения. Последние десятилетия широко стали использоваться новые материала при проектировании и создании новых технических структур. Такими материалами, например, являются эластомеры. Они могут испытывать большие упругие деформации. Это вызывает необходимость на стадии проектирования изделий применять нелинейную теорию упругости для расчета напряжений и деформаций. Нелинейная теория тонких оболочек, в которой используются гипотезы Кирхгоффа — Лява, стала разрабатываться еще в первой половине XX века [44].

Для материалов с нелинейными механическими свойствами с учетом экспериментальных данных [20, 22, 38, 39, 42, 48, 62, 65, 66, 73] были разработаны методы учета больших деформаций и методы решения нелинейных краевых задач [12–16, 18, 19, 25, 26, 49, 54, 58, 65, 80]. Это позволило решить конкретные статические задачи по растяжению резиновых мембран [21, 23, 40, 61, 63, 78, 79]. В последние годы теория оболочек нашла свое развитие в работах [2–5, 23, 47, 53, 68, 70, 72]. В дополнение к этому разрабатываются и модели оболочек и мембран, находящихся под давлением агрессивных сред [7, 17, 27–34, 43, 69, 71, 74].

Различные устройства, содержащие резиновые элементы, используются для гашения вибрационных нагрузок. Для систем, описываемых обыкновенными дифференциальными уравнениями, методы расчета амплитудно-частотных характеристик достаточно хорошо разработаны [8–11, 35–37, 41, 45, 67, 75–77]. В этой области решено много разных задач [1, 6, 46, 51, 52, 55–57, 59–60]. Для больших деформаций оболочек и мембран рассчитать такие характеристики не просто [12, 14, 16, 50, 64]. Это обусловлено не только трудностями построения решения нелинейных краевых задач, но и тем, что они задачи могут иметь и неединственное решение [12, 16, 20, 24, 50, 53]. Если задача имеет несколько решений, то возникают проблемы при построении численного решения таких краевых задач [16, 24].

Упругий потенциал. Внелинейной механике сплошных сред для описания свойств материалов используется потенциальная энергия деформации [13, 20, 42, 48, 65, 66, 73]. Для изотропного упругого материала она определяется как функция главных инвариантов деформации или как функция главных кратностей удлинения , и : . Для несжимаемого материала должно выполнять условие несжимаемости: . На основе экспериментальных исследований по растяжению образцов из резиноподобных материалов предлагались различные варианты упругого потенциала [20, 48, 65]. Как правило, считалось, что при малых деформациях эти потенциалы должны переходить в закон Гука для несжимаемого материала [20]. Образцы из резиноподобных материалов могут испытывать большие упругие деформации. Это должно учитываться в аналитическом выражении упругого потенциала. Поэтому при больших деформациях растяжения упругий потенциал как функция главных кратностей удлинения у разных авторов характеризуются разной степенью роста как функции главных кратностей удлинения [65, 73]. Одним из потенциалов, который обладает такими свойствами, является упругий потенциал [20]

(1)

где — начальный модуль сдвига, а рассматривается как постоянная материала. Этот потенциал представляет собой вариант потенциала Огдена [65]. При он переходит в неогуковский потенциалом [20, 73], при — в потенциал Бартенева-Хазановича [20].

Главные напряжения , и для несжимаемого материала определяются через частные производные от упругого потенциала по кратностям удлинения , и . В теории тонких оболочек используется гипотеза Кирхгофа о равенстве нулю напряжения . С учетом этого предположения напряжения и определяются следующим образом

, .

Уравнения движения мембраны. Рассмотрим в декартовой системе координат плоскую мембрану бесконечно длинную в направлении защемленную по двум сторонам (рис. 1) и нагруженную нормальным давлением [20]. Деформацию считаем не зависящей от координаты . В качестве независимой координаты принимаем . Координаты деформированной срединной поверхности в сечении обозначим через и , а толщину мембраны черз . Угол между осью и нормалью к срединной поверхности обозначим через . Тогда для координат срединной поверхности справедливы уравнения

, ,(2)

в которых — кратность удлинения в направлении дуги меридиана:

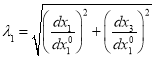.(3)

Поскольку деформации не зависят от , то . С учетом этого из условия несжимемости находится кратность деформационного изменения толщины мембраны .

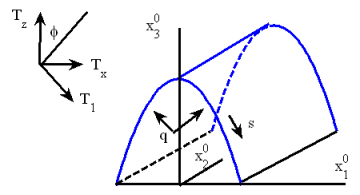
Рис. 1.

Пусть — сила внутренних напряжений, действующая по касательной к срединной поверхности. Силу внутренних напряжений, действующую по нормали к срединной поверхности, считаем равной нулю. Тогда проекции внутренних сил на координатные оси подсчитываются по формулам

, .(4)

Сила определяется через упругий потенциал

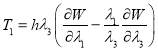.(5)

Уравнения движения примут вид

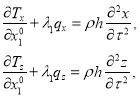(6)

где — проекция поверхностной нагрузки на ось , а — на ось , — плотность материала мембраны. Для нормального равномерного давления интенсивностью — , .

Примем, что толщина мембраны не зависит от координаты. Введем обозначения

,

и новые переменные

, , , .

Тогда уравнения (6) с учетом соотношений (2) — (5) примут вид

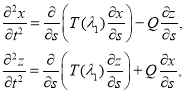
,(7)

, ,

.

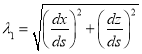К этим уравнениям добавляются граничные условия

при : , ,(8)

при : , .(9)

Эти условия означают, что край мембраны закреплен неподвижно, а край свободно перемещается в вертикальном направлении.

Статическое решение. Статистические уравнения равновесия получаются из уравнений (7) в предположении, что инерционные слагаемые в первых двух уравнениях равны нулю:

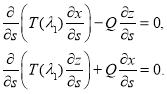(10)

С учетом граничных условий (8) — (9) отсюда находятся

, , , .(11)

Константы , , , и связаны соотношениями

, , . .(12)

Таким образом, деформированная поверхность мембраны в сечении представляет собой дугу окружности радиуса . Связь между давлением и кратностью удлинения определяется из соотношений (12).

Кратность удлинения при растяжении мембраны должна быть положительной величиной. Поэтому из первого соотношения в (12) следует, что должно выполняться неравенство . Тогда из третьего соотношения в (12) следует, что . Если усилие как функция растет медленнее, чем , тогда давление не может принимать бесконечно большие значения. То есть будет существовать такое критическое значение , что при значениях статические уравнения (10) решений иметь не будут. Зависимость в этом случае должна иметь точку максимума. Для упругого потенциала (1) на рис. 2 показана эта зависимость для значений . В экспериментальных исследваниях по растяжению круглых мембран нормальным давлением такая зависимость реализуется [20, 22, 40, 50, 63, 78, 79].

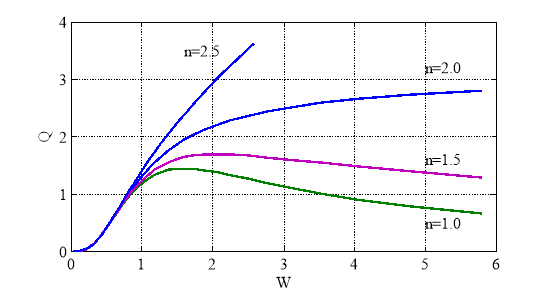
Рис. 2. Зависимость «давление — максимальный прогиб» для значений параметра в упругом потенциале (1)

Малые колебания около положения равновесия. Усилие в случае статических уравнений является постоянной величиной и не зависит от координаты . Будем считать, что около положения равновесия, которое описывается уравнениями (7), возникают малые колебания. При этом примем, что кратность удлинения и усилие постоянные величины, определяемые из соотношений (11) — (12). Тогда первые два уравнения в (7) с учетом соотношений (11) — (12) приводится к виду

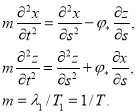(13)

Периодическое во времени решение этих уравнений ищется в виде произведения двух функций, одна из которых зависит от , а вторая от :

.

Тогда из (1) и (8) — (9) находим, что функции и должны удовлетворять системе уравнений

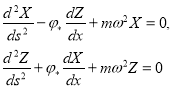(14)

и граничным условиям

, , , .(15)

Решение уравнений (14), удовлетворяющее граничным условиям (15), представляется в виде

, ,

где есть произвольные постоянные, удовлетворяющие системе линейных однородных уравнений

.

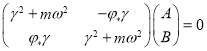Эта система уравнений будет иметь нетривиальное решение, если ее определитель обращается в ноль:

.

Из этого уравнения находятся

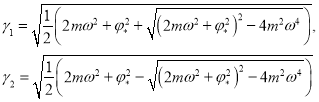
и решение уравнений (14), удовлетворяющее условиям (15), представляется в виде

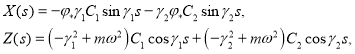
где и — произвольные постоянные. Граничные условия при будут удовлетворены, если выполняется равенство

,

которое и является уравнением для нахождения .

На рис. 3 показана зависимость первых четырех частот собственных колебаний от для неогуковского потенциала, а на рис. 4 — зависимость первой частоты собственных колебаний от для потенциала (1) с , , и .

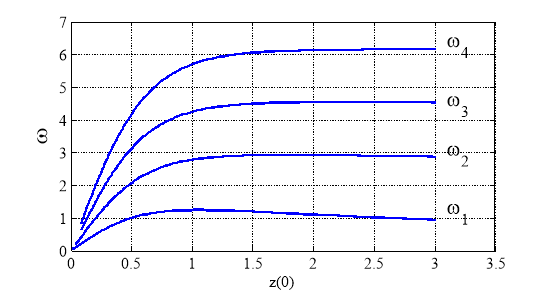
Рис. 3. Зависимость первых четырех частот собственных колебаний от для неогуковского потенциала

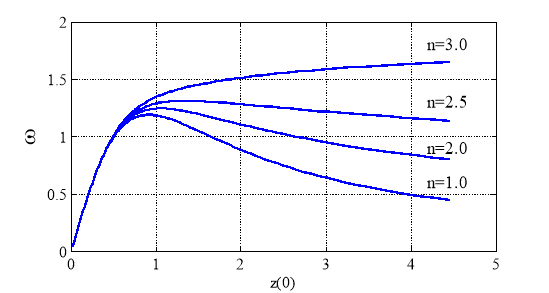
Рис. 4. Зависимость первой частоты собственных колебаний от для потенциала (1) с , , и

Нелинейные уравнения. Всамом общем случае построить аналитическое решение для уравнений динамики (7) не удается. Поэтому для нахождения решения при заданных граничных и начальных условиях использовались численные методы [16, 24, 25]. Динамические уравнения (7) решались с применением метода сеток. Дискретизация уравнений на сетке

осуществлялось как по пространственной, так и по временной переменной конечными разностями: на внутренних узлах пространственной сетки

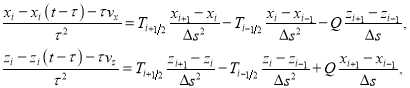(16)

, (),

на границе :

.

на границе :

.

Скорости и подсчитывалась следующим образом

, .

Значения , , и в (16) вычисляются в момент времени . Поэтому система уравнений (16) является нелинейной. Ее решение на каждом временном шаге решалась итерационным методом.

При построении решения для случая малых колебаний в окрестности статического положения равновесия, описываемого соотношениям (16), определялся период колебаний в зависимости от прогиба мембраны в точке . Эта зависимость для случая потенциала (1) с , и приведена на рис. 5. Зависимость периода перемещения точки для неогуковского потенциала для случая точного решения и решения линейных уравнений (13) приведена на рис. 6.

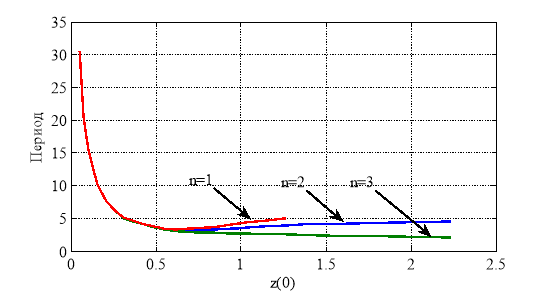
Рис. 5. Зависимость изменения периода колебаний точки для потенциала (1) с , и

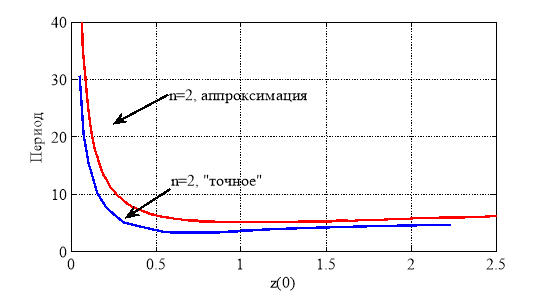
Рис. 6. Зависимость периода перемещения точки для неогуковского потенциала для случая точного решения и решения линейных уравнений (13)

Решение нелинейных уравнений (16) при начальных условиях

, , ,

строилось при разбиении промежутка интегрирования по пространственной переменной на 100, 500 и 5000 отрезков. Шаг интегрирования по временной переменной выбирался из условия . Некоторые из результатов решения представлены на рис. 7–9 для значения . На рис. 7 показан вид мембраны в сечении в моменты времени . На начальной стадии растяжения мембраны (рис. 7, ) центральная часть мембраны остается «прямолинейной». В момент времени значение функции в точке как функции времени достигает максимального значения. Форма мембраны в этот момент времени близка к цилиндрический. В дальнейшем начинается возвращение мембраны в исходное положение равновесия (рис. 8, ). В окрестности исходного положения равновесия скорость возврата точек центральной части мембраны становится больше, чем в некоторой части внутри промежутка (рис. 8, ). Причиной этого, по-видимому, является то, что скорость перемещений точек мембраны в вертикальном направлении и скорость распространения возмущения вдоль срединной поверхности не одинаковы.

На рис. 9 показана зависимость функций и от времени. Как следует из этого результата в точке достигает своего максимального значения раньше, чем максимальное значение достигнет в этой точке . То есть «подъем» этой точки начинает сопровождаться увеличением толщины мембраны в ее окрестности — возмущение толщины в начальный момент времени в окрестности точки (рис. 8, ) достигает точки раньше, чем прогиб в точке достигнет максимальное значения. Это возмущение в точке отразиться, и начнет распространяться назад к точке . В общей сложности одному «периоду» колебаний мембраны в вертикальном направлении соответствуют два периода колебаний точек мембраны вдоль срединной поверхности. Это и объясняет форму мембраны с двумя экстремумами (рис. 8, ).

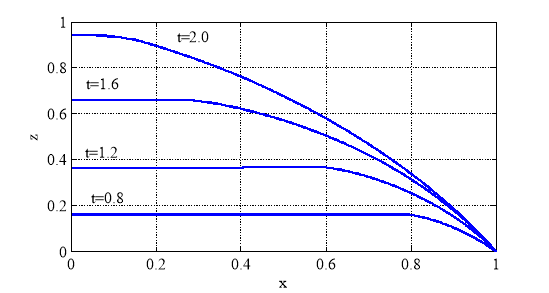
Рис. 7. Форма мембраны в моменты времени для неогуковского потенциала

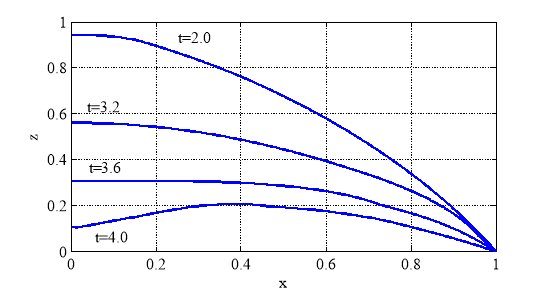
Рис. 8. Форма мембраны в моменты времени для неогуковского потенциала

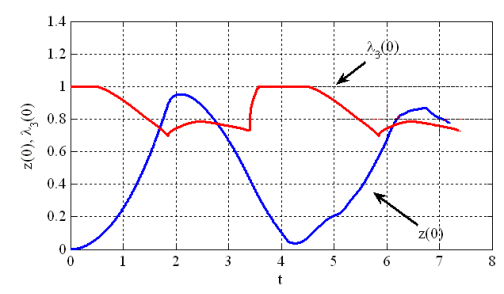
Рис. 9. Зависимость прогиба мембраны и ее толщины в центре от времени для неогуковского потенциала.

Таким образом, нелинейные динамические модели дают более сложную картину колебаний мембран, чем линейные.

Заключение. Математические модели линейных и нелинейных колебаний мембран могут дать не только количественные отличия в решениях, но и качественные. При малых колебаниях около статического положения равновесия для определения частот собственных колебаний можно использовать линеаризованные решения. Построение численного решения нелинейных уравнений эффективно можно строить с применением сеточных методов, используя технологии параллельных вычислений.

Литература:

1. Абдулина, К. А., Старков В. Н. Качественное исследование динамики лесной системы с учетом вырубки и вывоза // Процессы управления и устойчивость. — 2014. — Т. 1. — № 1. — С. 82–86.
2. Гасратова, Н. А. Напряженно-деформированное состояние упругого пространства со сферическим жестким включением // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2009. — № 1. — С. 14–18.
3. Гасратова, Н. А. Решение некоторых классических пространственных задач теории упругости в напряжениях // Молодой ученый. — 2014. — № 3 (62). — С. 1–6.
4. Гасратова, Н. А., Шамина В. А. Об одном подходе к решению осесимметричных задач линейной теории упругости // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2007. — № 2. — С. 101–106.
5. Гасратова, Н. А., Шамина В. А. Решение в напряжениях линейной осесимметричной задачи для сферы и упругого пространства со сферической полостью // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2008. — № 2. — С. 122–128.
6. Гасратова, Н. А., Гасратов М. Г. Сетевая модель управления запасами для случая количественной конкуренции // Сибирский журнал индустриальной математики. — 2015. — Т. 18. — № 1. — С. 14–27.
7. Даль, Ю. М., Пронина Ю. Г Сосредоточенные силы и моменты у границы упругой полуплоскости // Известия Российской академии наук. Механика твердого тела. — 1998. — № 5. — С. 78.
8. Екимов, А. В., Жабко А. П., Смирнов Н. В. Матричный анализ эргодических полу марковских процессов // Вестник Санкт-Петербургского университета. Серия 10. Прикладная математика. Информатика. Процессы управления. — 2004. — № 1–2. — С. 16–29.
9. Екимов, А. В. Анализ множества достижимости нелинейных управляемых систем // Естественные и математические науки в современном мире. — 2014. — № 15. — С. 8–13.
10. Екимов, А. В. К вопросу об ограниченности интегральной воронки в билинейных управляемых системах // Системы управления и информационные технологии. — 2014. — Т. 56. — № 2.1. — С. 138–142.
11. Екимов, А. В. К вопросу об эргодическом поведении полумарковского случайного процесса // Труды математического центра имени Н. И. Лобачевского. — 2013. — Т. 46. — № 11. — С. 185–186.
12. Кабриц, С. А. Некоторые прикладные задачи статики тонких оболочек из эластомеров // диссертация на соискание ученой степени кандидата физико-математических наук / Ленинград, 1984.
13. Кабриц, С. А., Мальков В. М., Мансурова С. Е. Нелинейные уравнения плоского слоя для трех моделей эластомерного материала // Известия Российской академии наук. Механика твердого тела. — 2001. — № 1. — С. 38.
14. Кабриц, С. А., Черных К. Ф. Нелинейная теория изотропно упругих тонких оболочек с учетом поперечного сдвига // Известия Российской академии наук. Механика твердого тела. — 1996. — № 1. — С. 124.
15. Кабриц, С. А., Шамина В. А. Изгиб оболочки вращения поперечной силой и моментом // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2014. — № 2. — С. 261–270.
16. Кабриц, С. А., Колпак Е. П. О численном построении бифуркационных ветвей в нелинейных задачах статики оболочек // В сборнике: Устойчивость и процессы управления Материалы III международной конференции. 2015. — С. 360–361.
17. Камачкин, А. М., Старков В. Н., Степенко Н. А. Математическая модель загрязнения океанических вод // Вестник Тамбовского университета. Серия: Естественные и технические науки. — 2015. — Т. 20. — № 2. — С. 475–479.
18. Колпак, Е. П. Matlab: методы вычислений учебное пособие / Е. П. Колпак; Санкт-Петербургский гос. ун-т. Санкт-Петербург, 2007.
19. Колпак, Е. П. Введение в механику сплошных сред учебное пособие / Е. П. Колпак; С.-Петерб. гос. ун-т. СПб. 2004.
20. Колпак,Е. П. Устойчивость и закритические состояния безмоментных оболочек при больших деформациях // диссертация на соискание ученой степени доктора физико-математических наук / Санкт-Петербург, 2000.
21. Колпак, Е. П., Мальцева Л. С. Большие деформации резиновых мембран // Молодой ученый. — 2014. — № 16 (75). — С. 78–84.
22. Колпак, Е. П., Мальцева Л. С. Круглая плоская мембрана при больших деформациях // Приволжский научный вестник. — 2014. — № 11–1 (39). — С. 5–10.
23. Колпак, Е. П., Мальцева Л. С Эластомерные мембраны при больших деформациях // В сборнике: Устойчивость и процессы управления Материалы III международной конференции. 2015. — С. 362–363.
24. Матросов, А. В. Вычислительная неустойчивость алгоритма метода начальных функций // Вестник Санкт-Петербургского университета. Серия 10. Прикладная математика. Информатика. Процессы управления. — 2010. — № 4. — С. 30–39.
25. Матросов, А. В. Расчет балочных перекрытий численно-аналитическим методом // Вестник государственного университета морского и речного флота им. адмирала С. О. Макарова. — 2012. — № 1. — С. 8–15.
26. Олемской, И. В. Явный метод типа Рунге — Кутты пятого порядка // Вычислительные технологии. — 2005. — Т. 10. — № 2. — С. 87–105.
27. Пронина, Ю. Г Механохимическая коррозия полого цилиндра из идеального упруго-пластического материала под действием постоянного давления // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2006. — № 3. — С. 121–130.
28. Пронина, Ю. Г. Влияние поверхностных факторов на напряженно-деформированное состояние твердых тел с отверстиями // диссертация на соискание ученой степени доктора физико-математических наук / Санкт-Петербургский государственный университет. Санкт-Петербург, 2010.
29. Пронина, Ю. Г. Краевая дислокация и сосредоточенная сила в упругой полуплоскости с отверстиями и краевыми вырезами // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2012. — № 4. — С. 120–124.
30. Пронина, Ю. Г. О сосредоточенных воздействиях у границы упругой пластины // Труды ЦНИИ им. акад. А. Н. Крылова. — 2010. — № 53. — С. 117–122.
31. Пронина, Ю. Г. Равномерная механохимическая коррозия полой сферы из идеального упругопластического материала под действием постоянного давления // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2009. — № 1. — С. 113–122.
32. Пронина, Ю. Г. Расчет долговечности упругой трубы под действием продольной силы, давления и осесимметричного нагрева в условиях равномерной коррозии // Проблемы прочности и пластичности. — 2009. — № 71. — С. 129–135.
33. Пронина, Ю. Г. Центры расширения-сжатия в упругой полуплоскости // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2007. — № 2. — С. 140–149.
34. Пронина, Ю.Г Оценка устойчивости упругой трубы под давлением коррозионных сред // Вестник Санкт-Петербургского университета. Серия 10. Прикладная математика. Информатика. Процессы управления. — 2006. — № 3. — С. 55–63.
35. Старков, В. Н., Степенко Н. А. Исследование динамики маятниковых систем с переменными параметрами // Естественные и математические науки в современном мире. — 2014. — № 15. — С. 20–36.
36. Степенко, Н. А. О диссипативности неавтономных систем по нелинейному приближению // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2004. — № 3–4. — С. 160–169.
37. Степенко, Н. А. О некоторых критериях диссипативности колебательных систем с переменными параметрами // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2004. — № 1. — С. 50–54.
38. Шиманчук, Д. В. Моделирование орбитального управляемого движения космического аппарата в окрестности коллинеарной точки либрации L1 // Вестник Санкт-Петербургского университета. Серия 10. Прикладная математика. Информатика. Процессы управления. — 2010. — № 3. — С. 86–92.
39. Albrecht, A. B., Ravi-Chandar, K. High strain rate response of rubber membranes // Journal of the Mechanics and Physics of Solids. — 2014. — V. 64. — P. 377–395.
40. Balakhovsky, K., Volokh, K. Y. Inflation and rupture of rubber membrane // International Journal of Fracture. — 2012. — Т. 177. — С. 179–190.
41. Balykina, Y. E., Kolpak E. P., Kotina E. D. Mathematical model of thyroid function // Middle East Journal of Scientific Research. — 2014. — Т. 19. — № 3. — С. 429–433.
42. Chagnon, G., Rebouah, M., Favier, D Hyperelastic Energy Densities for Soft Biological Tissues: A Review // Journal of Elasticity. 2015. — М. 120. — P. 129–160.
43. Dal' Yu. M., Pronina Yu. G. On concentrated forces and moments in an elastic half-plane // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 1998. — № 1. — С. 57–60.
44. Donnell, E. H. A new the oryforthebuckling of thin cylinders under axial compression and bending // Transactions of the ASME. — 1934. — V. 56. — P. 795–806.
45. Ekimov, A. V. Qualitative analyses of attainability set of nonlinear controllable systems // Proc. 20th Int. Workshop Beam Dynamics and Optimization, St. Petersburg, Russia, 2014, p. 51.
46. Feng, C., Yu L., Zhang W. Dynamic analysis of a dielectric elastomer-based microbeam resonator with large vibration amplitude // International Journal of Non-Linear Mechanics. — 2014. — V. 65. — P. 63–68.
47. Gasratova, N. A. Study of building an analytical solution of the axisymmetric problem of linear elasticity in stresses as exemplified by finding the stress-strainstate of an ellipsoid cocavityunder the inner pressure // ARPN Journal of Engineering and Applied Sciences. — 2014. — Т. 9. — № 11. — С. 2259–2267.
48. Gent, A. N., A new constitutive relation for rubber // Rubber Chem. Technol. — 1996. — V. 69. — P. 59–61.
49. Hansbo, P., Larson, M.G., Larsson, F. Tangential differential calculus and the finite element modeling of a large deformation elastic membrane problem // Computational Mechanics. — 2015. — V. 56. — P. 87–95.
50. Ingo, Muller Two Instructive Instabilities in Non-Linear Elasticity: Biaxially Loaded Membrane, and Rubber Balloons // Meccanica. — 1996. — V. 31: — P. 387–395.
51. Ivanov, G. G., Sharlay A. S. On stability of linear homogeneous switched systems // В сборнике: 2015 International Conference «Stability and Control Processes» in Memory of V. I. Zubov (SCP) 2015. — С. 13–15.
52. Ivanov, S E., Melnikov V. G., On the equation of fourth order with quadratic nonlinearity // International Journal of Mathematical Analysis. — 2015. — Т. 9. — №. 54. — С. 2659–2666.
53. Kabrits, S. A., Kolpak E. P. Finding bifurcation branches in nonlinear problems of statics of shells numerically // В сборнике: 2015 International Conference «Stability and Control Processes» in Memory of V. I. Zubov (SCP) 2015. — С. 389–391.
54. Kabrits, S. A., Kolpak E. P. Numerical study of convergence of nonlinear models of the theory of shells with thickness decrease // В сборнике: AIP Conference Proceedings. — 2015. — С. 300005.
55. Kabrits, S. A., Slepneva L. V. Small nonsymmetric oscillations of viscoelastic damper under massive body action // Вестник Санкт-Петербургского университета. Серия 1. Математика. Механика. Астрономия. 1998. — № 2. — С. 78
56. Kolpak, E. P., Ivanov S. E. Mathematical and computer modeling vibration protection system with damper // Applied Mathematical Sciences. — 2015. — Т. 9. — № 78. — С. 3875–3885.
57. Kolpak, E. P., Maltseva L. S., Ivanov S. E., On the stability of compressed plate // Contemporary Engineering Sciences. — 2015. — Т. 8. — № 20. — С. 933–942.
58. Kolpak, E. P., Kabrits S. A., Bubalo V. The follicle function and thyroid gland cancer // Biology and Medicine. — 2015. — Т. 7 (1). — BM060.15.
59. Kolpak, E. P., Ivanov S. E. Mathematical and computer modeling vibration protection system with damper // Applied Mathematical Sciences. — 2015. — Т. 9. — № 77–80. — С. 3875–3885.
60. Kolpak, E. P., Ivanov S. E. Mathematical modeling of the system of drilling rig // Contemporary Engineering Sciences. — 2015. — Т. 8. — № 13–16. — С. 699–708.
61. Kolpak, E. P., Maltseva L. S., Ivanov S. E. On the stability of compressed plate // Contemporary Engineering Sciences. — 2015. — Т. 8. — № 20. — С. 933–942.
62. Kolpak, E. P., Maltseva, L. S., 2015, Rubberlike membranes at inner pressure // Contemporary Engineering Sciences. — 2015. — Т. 8. — № 36. –С. 1731–1742.
63. Landon, M., Kanner M, Cornelius O. Horgan Elastic instabilities for strain-stiffening rubber-like spherical and cylindrical thin shells under inflation // International Journal of Non-Linear Mechanics. — 2007. — № 42. — С. 204. — 215.
64. Li, Q., Zhu, Y., Xu, D., Hu, J., Min, W., Pang, L. A negative stiffness vibration isolator using magnetic spring combined with rubber membrane // Journal of Mechanical Science and Technology. –Т. 27. ‑№ 3. — С. 813–824.
65. Ogden, R. W., Saccomandi G., Sgura I. Fitting hyperelastic models to experimental data // Comput. Mech. — 2004. — № 34. — 484–502.
66. Paimushin, V. N., Firsov V. A., Gyunal I., Egorov A. G. Theoretical-experimental method for determining the parameters of damping based on the study of damped flexural vibrations of test specimens. 1. Experimental basis // Mechanics of Composite Materials. — 2014. — Т. 50. — № 2. — С. 127–136.
67. Polyakhova, E. N., Starkov V. N., Stepenko N. A. Solar sailing out of ecliptic plane // В сборнике: 2015 International Conference «Stability and Control Processes» in Memory of V. I. Zubov (SCP) 2015. — С. 65–68.
68. Pronina, Y. G. Analytical solution for decelerated mechanochemical corrosion of pressurized elastic-perfectly plastic thick-walled spheres // Corrosion Science. — 2015. — Т. 90. — С. 161–167.
69. Pronina, Y. G. Lifetime assessment for an ideal elastoplastic thick-walled spherical member under general mechanochemical corrosion conditions // Computational Plasticity XII: Fundamentals and Applications — Proceedings of the 12th International Conference on Computational Plasticity — Fundamentals and Applications, COMPLAS 2013. — PP. 729–738.
70. Pronina, Y. G. Analytical solution for decelerated mechanochemical corrosion of pressurized elastic-perfectly plastic thick-walled spheres // Corrosion Science. — 2015. — Т. 90. — С. 161–167.
71. Pronina, Y. G. Thermoelastic stress analysis for a tube under general mechanochemical corrosion conditions // В сборнике: Proceedings of the 4th International Conference on Computational Methods for Coupled Problems in Science and Engineering, COUPLED PROBLEMS 2011 2011. — С. 1408–1415.
72. Pronina, Y. G., Sedova O. S., Kabrits S. A On the applicability of thin spherical shell model for the problems of mechanochemical corrosion // AIP Conference Proceedings. — 2015. — vol. 16–48. — art. no. 300008.
73. Rivlin, R. S., Large elastic deformations of isotropic materials. VI. Further results in the theory of torsion, shear and flexure // Philos. Trans. R. Soc. London, Ser. A 42 (1949) 173–195.
74. Sedova, O., Pronina Y. Generalization Of The Lamé Problem For Three-Stage Decelerated Corrosion Process Of An Elastic Hollow Sphere // Mechanics Research Communications. — 2015. — Т. 65. — С. 30–34.
75. Starkov, V. N., Stepenko N. A., Computer modeling of trajectories in spatially non-uniform gravitational fields, 2014 International Conference on Computer Technologies in Physical and Engineering Applications, ICCTPEA 2014 — Proceedings 6893345, 175–176.
76. Starkov, V. N., Stepenko N. A. Computer modeling of trajectories in spatially non-uniform gravitational fields // International conference on computer technologies in physical and engineering applications (IVESC-ICEE-ICCTPEA-BDO 2014). June 30-July 4. 2014, Russia, Saint-Petersburg, pp. 179–180.
77. Starkov, V. N., Stepenko N. A. Simulation of particle motion in the given speed fields // В сборнике: 2015 International Conference «Stability and Control Processes» in Memory of V. I. Zubov (SCP) 2015. — С. 75–77.
78. Tuzel, V. H., Erbay H. A. Dynamic extension of a compressible nonlinearly elastic membrane // IMA Journal of Applied Mathematics. — 2005. — № 70. — С. 25–38.
79. Wineman, A. Some results for generalized neo-Hookean elastic materials // International Journal of Non-Linear Mechanics. — 2005. — Т. 40. С. — 271–279.
80. Zhukova, I. V., Kolpak E. P., Balykina Yu. E. Mathematical Model of Growing Tumor // Applied Mathematical Sciences. — 2014. — Т. 8. — N 29–32. — С. 1455–1466.