Введение. Первые математические модели конкуренции, разработанные для биологических популяций, принадлежат, по-видимому, Вольтерра [15]. В рамках этих моделей в условиях конкуренции «выживает» тот вид, который при прочих равных условиях быстрее остальных размножается. Однако в среде биологических популяций есть множество примеров [10, 22, 90] «мирно» существующих на одном и том же трофическом ресурсе видов с разными скоростями воспроизводства потомства. Постоянное конкурентное подавление одного сообщества другим должно было бы значительно уменьшить число видов. Однако факт существования в природе множества животных и растений не согласуется, в целом, с этой гипотезой [90]. Обилие видов можно объяснить и тем, что конкуренция была в прошлом и со временем виды нашли свои экологические ниши в виде иных трофических ресурсов и мест обитаний.
Существование в биоценозах множества не погибающих из-за конкуренции видов можно объяснить наличием у каждого из них своей экологической ниши [10, 22, 53]. То есть, модель Вольтерра объясняет, по-видимому, один из возможных вариантов эволюции взаимодействующих популяций. Последователями Вольтерра были разработаны модели, которые допускали одновременное устойчивое существование двух конкурирующих видов [4, 10, 98]. То есть предлагались варианты описания «выживания слабых видов» среди «сильных», которые с точки зрения модели конкуренция Вольтерра должны были бы погибнуть.
В системе экономических взаимоотношений, как и в системе взаимоотношений между популяциями в биоценозах, между производителями товаров и услуг существует конкуренция [22, 53, 68]. Конкуренция носит разнообразный характер, по-разному влияет на эволюцию производств и систему перераспределения ресурсов [32, 33, 38, 80, 85]. Производители материальных ценностей ищут различные способы уменьшения внутренних потерь («внутренняя конкуренция») [5, 21, 25, 62, 65, 72, 77, 78, 83] и ослабления внешних факторов («межвидовая конкуренция»), мешающих увеличению собственных материальных ценностей [28, 54, 56, 61, 67, 74, 79, 82, 86, 87, 93, 94]. В экономической системе взаимоотношений производители, в конечном итоге, также ищут свою «экономическую нишу». Аналогичные процессы происходят и на международном рынке товаров и услуг. Здесь происходит самоорганизация производителей внутри страны, приводящая к такому перераспределению реализуемых ресурсов, при котором потребность в них на международном рынке постоянно растет, несмотря на конкуренцию между странами. Например, оборот внешней торговли России с 1995 года по 2013 год постоянно возрастал [73]. На рис. 1 отражена динамика объема экспорта внешней торговли со странами ближнего и дальнего зарубежья, на рис. 2 — импорта. Небольшое падение оборота торговли в 1990-е годы объясняется падением производства в стране, а падение в 2008–2010 годы — финансовым кризисом 2008 года. В целом объемы торговли постоянно растут (рис. 1–2). То есть, судя по этому показателю, с 1995 по 2013 год конкуренция на международном рынке не оказывала влияние на торговой оборот России.
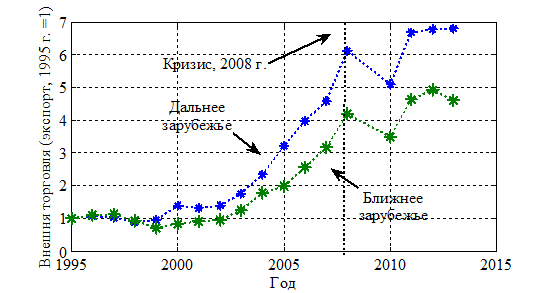
Рис. 1.
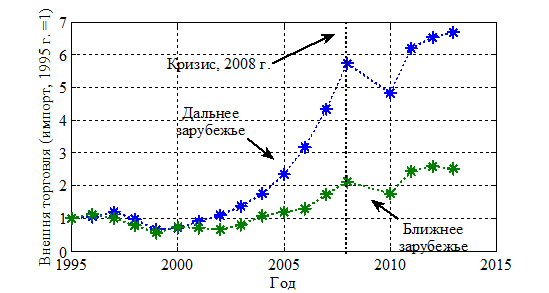
Рис. 2.
Наряду с моделями конкуренции Вольтерра были разработаны и иные математические модели биологических сообществ, в которых учитывались и конкурентные взаимоотношения [2–4, 6–8, 16, 30, 31, 37, 41, 47, 48, 57, 84, 88, 92, 97, 99], и модели конкуренции в системе экономических взаимоотношений [11, 12, 14, 35, 66]. Ниже предлагаются варианты математических моделей ухода от конкуренции или, другими словами, уход популяции в другую экологическую нишу.
Математическая модель конкуренции (Вольтера — Бигон). Для описания динамики численности двух конкурирующих популяций используется «модифицированная» математическая модель Вольтерра, учитывающая как межвидовую, так и внутривидовую конкуренцию [4, 10, 47]
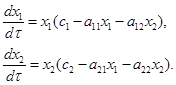 (1)
(1)
В этих уравнениях 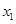 и
и 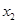 — численности двух конкурирующих популяций,
— численности двух конкурирующих популяций, 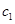 ,
, 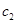 ,
, 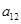 ,
, 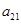 ,
, 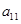 и
и 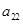 — положительные постоянные,
— положительные постоянные, 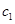 и
и 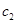 — удельные скорости роста популяций при их малой численности,
— удельные скорости роста популяций при их малой численности, 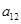 и
и 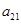 — коэффициенты, определяющие скорость уменьшения численности популяций за счет межвидовой конкуренции, а
— коэффициенты, определяющие скорость уменьшения численности популяций за счет межвидовой конкуренции, а 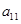 и
и 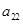 — за счет внутривидовой конкуренции [4, 10, 47].
— за счет внутривидовой конкуренции [4, 10, 47].
Система уравнений (1) заменой [2]
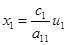 и
и 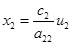
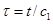
приводятся к виду
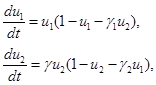 (2)
(2)
где 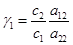 ,
, 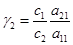 ,
, 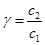 .
.
Система уравнений (2) имеет четыре стационарные точки [4, 10, 47]
1. 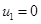 ,
, 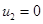 .
.
2. 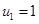 ,
, 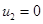 .
.
3. 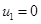 ,
, 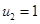 .
.
4. 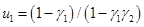 ,
, 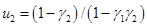 , если
, если  и
и  или
или  и
и  .
.
Первая стационарная точка является неустойчивой, вторая будет устойчивой, если 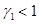 и
и 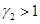 , а третья, если
, а третья, если 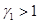 и
и 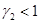 . Четвертая стационарная точка реализуется и будет устойчивой, если
. Четвертая стационарная точка реализуется и будет устойчивой, если 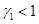 и
и 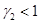 .
.
Неравенство 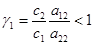 , а это условие существования первой популяции в условиях конкуренции, обеспечивается большей скоростью роста ее численности по сравнению со скоростью роста численности второй популяции (
, а это условие существования первой популяции в условиях конкуренции, обеспечивается большей скоростью роста ее численности по сравнению со скоростью роста численности второй популяции (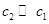 ) и меньшим влиянием на нее второй популяции (
) и меньшим влиянием на нее второй популяции (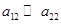 ). При этом если внутривидовая конкуренция значительно меньше межвидовой (
). При этом если внутривидовая конкуренция значительно меньше межвидовой (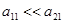 ) настолько, что выполнится неравенство
) настолько, что выполнится неравенство 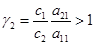 , то вторая популяция может погибнуть.
, то вторая популяция может погибнуть.
В четвёртой стационарной точке собственные значения матрицы Якоби правой части уравнений (2), являющиеся корнями квадратного уравнения
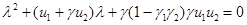 ,
,
отрицательные. Поэтому эта стационарная точка будет устойчивой.
Таким образом, модель конкуренции (2) допускает одновременное устойчивое существование двух популяций.
«Активный» уход от конкуренции. Эволюция видов происходила таким образом, что под влиянием внешних факторов и внутренних изменений в организмах отдельных особей изменялся внутренний метаболизм, и они постепенно начинали использовать новые трофические ресурсы [10, 22]. При этом виды продолжали существовать совместно. Это можно учесть, считая, что в модели (2) 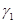 и
и 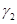 функциями времени. Тогда модель «ухода» от конкуренции принимает вид
функциями времени. Тогда модель «ухода» от конкуренции принимает вид
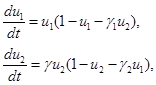
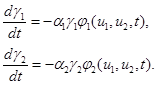
В этой модели предполагается, что 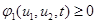 и
и 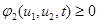 . То есть считается, что функции
. То есть считается, что функции 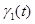 и
и 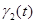 не возрастающие функции времени. Это обеспечивает постепенный «уход от конкурентных взаимоотношений». Принятие в качестве функций
не возрастающие функции времени. Это обеспечивает постепенный «уход от конкурентных взаимоотношений». Принятие в качестве функций 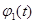 и
и 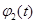
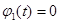 , если
, если 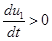 , и
, и 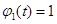 , если
, если 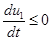 ,
,
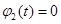 , если
, если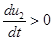 , и
, и 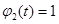 , если
, если 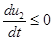
означает, что популяции «чувствуют» уменьшении их численности и сразу «реагируют» на это. В этой модели предполагается, что каждая популяции пытается уменьшить влияние на себя конкурирующей с ней популяции.
На рис. 3 для случая 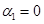 ,
, 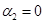 ,
, 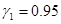 ,
, 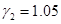 ,
, 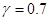 (модель (1)) отражены зависимости
(модель (1)) отражены зависимости 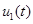 и
и 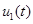 (кривые 1), для случая
(кривые 1), для случая 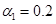 ,
, 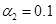 ,
, 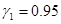 ,
, 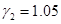 ,
, 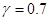 этим же зависимостям соответствуют кривые 2 в рассматриваемой модели. Выбранный набор постоянных
этим же зависимостям соответствуют кривые 2 в рассматриваемой модели. Выбранный набор постоянных 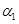 ,
, 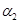 ,
, 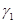 ,
, 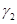 в модели (1) соответствуют случаю гибели второй популяции (рис. 3, кривые 1).
в модели (1) соответствуют случаю гибели второй популяции (рис. 3, кривые 1).
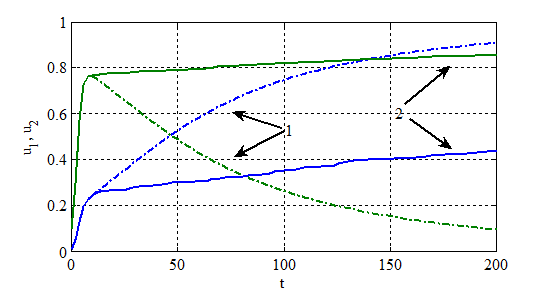
Рис. 3.
«Пассивный» уход от конкуренции. В этой модели предполагается, что уход от конкуренции происходит «естественным» путем
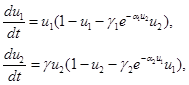 (3)
(3)
Слагаемое 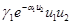 в первом уравнении — скорость уменьшения численности первой популяций вызванная конкуренцией, а слагаемое
в первом уравнении — скорость уменьшения численности первой популяций вызванная конкуренцией, а слагаемое 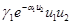 во втором уравнении — скорость уменьшения второй популяций обусловленная конкуренцией.
во втором уравнении — скорость уменьшения второй популяций обусловленная конкуренцией.
Нетривиальная стационарная точка системы уравнений (3), в которой 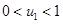 и
и 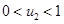 , находится как решение системы уравнений
, находится как решение системы уравнений
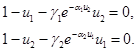 (4)
(4)
Функция 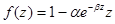 в точке
в точке 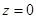 положительна (
положительна (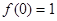 ) и является убывающей (
) и является убывающей (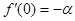 ), а в точке
), а в точке 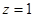 будет принимать положительные значения, если выполняется неравенство
будет принимать положительные значения, если выполняется неравенство 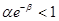 . При выполнении неравенства
. При выполнении неравенства 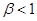 на промежутке
на промежутке 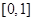
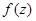 будет монотонно убывающей функцией. При одновременном выполнении неравенств
будет монотонно убывающей функцией. При одновременном выполнении неравенств 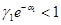 ,
, 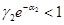 ,
, 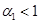 и
и 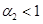 система уравнений (4) будет иметь единственное решение, удовлетворяющее условиям
система уравнений (4) будет иметь единственное решение, удовлетворяющее условиям 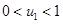 и
и 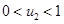 . При выполнении неравенства
. При выполнении неравенства 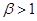 функция
функция 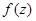 будет иметь минимум на промежутке
будет иметь минимум на промежутке 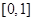 в точке
в точке 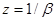 . Поэтому при выполнении неравенства
. Поэтому при выполнении неравенства 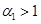 или
или 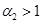 система уравнений (4), в зависимости от значений постоянных, входящих в уравнения (3), может иметь два решения, удовлетворяющих условиям
система уравнений (4), в зависимости от значений постоянных, входящих в уравнения (3), может иметь два решения, удовлетворяющих условиям 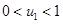 и
и 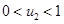 . Таким образом в этой модели могут существовать три стационарные точки.
. Таким образом в этой модели могут существовать три стационарные точки.
Собственные значения матрицы Якоби правой части уравнений (3) являются корнями полинома
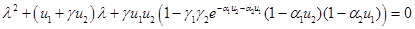 .
.
При одновременном выполнении неравенств 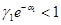 ,
, 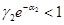 ,
, 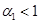 и
и 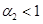 свободный член этого полинома положителен его корни будут иметь отрицательные вещественные части и, соответственно, нетривиальная стационарная точка будет устойчивой.
свободный член этого полинома положителен его корни будут иметь отрицательные вещественные части и, соответственно, нетривиальная стационарная точка будет устойчивой.
Сезонность конкуренции. Интенсивность потребления общего трофического ресурса популяциями может изменяться во времени. Это зависит от периодичности рождения потомства, физических возможностей особей, климатических условий и других причин [10]. То есть интенсивность конкурентных взаимоотношений может зависеть от времени [10]. Учесть это в модели (2) можно, полагая 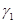 и
и 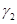 функциями, зависящими от времени
функциями, зависящими от времени
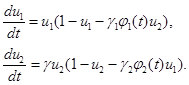
Для случая функций
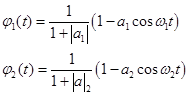
где 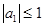 и
и 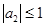 , результаты решения уравнений в виде зависимостей
, результаты решения уравнений в виде зависимостей 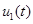 и
и 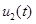 для случая
для случая 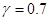 ,
, 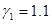 ,
, 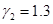 ,
, 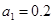 ,
, 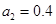 ,
, 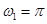 ,
, 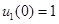 ,
, 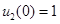 представлены на рис. 4–5. Рис. 4 соответствует
представлены на рис. 4–5. Рис. 4 соответствует 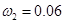 , а рис. 5 —
, а рис. 5 — 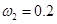 . В качестве начальных условий взяты
. В качестве начальных условий взяты 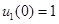 и
и 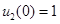 . Это соответствует случаю, когда конкурентные взаимоотношения начинаются в начальный момент времени при максимальных значениях
. Это соответствует случаю, когда конкурентные взаимоотношения начинаются в начальный момент времени при максимальных значениях 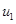 и
и 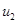 . При принятых значениях
. При принятых значениях 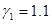 и
и 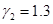 в случае
в случае 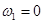 и
и 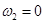 , как это следует из анализа уравнений (1), одновременное устойчивое существование двух популяций невозможно, а в рассматриваемой модели совместное существование с периодическим изменением численности возможно.
, как это следует из анализа уравнений (1), одновременное устойчивое существование двух популяций невозможно, а в рассматриваемой модели совместное существование с периодическим изменением численности возможно.
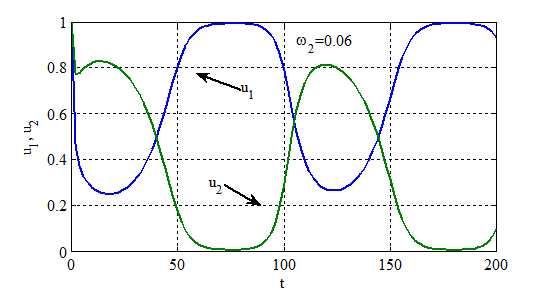
Рис. 4.
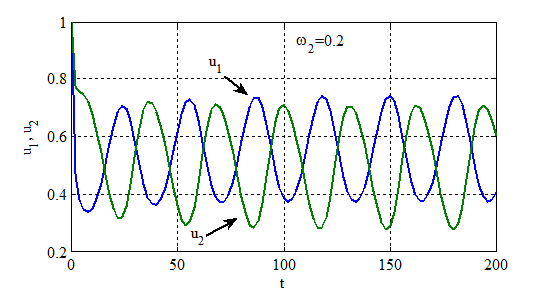
Рис. 5.
Смена ареала. При наличии конкуренции один из видов может постепенно уйти от конкурентных взаимоотношений на другой трофический ресурс [10, 21]. Пусть две конкурирующие популяции существуют на общей территории или одном трофическом ресурсе, а одна из них может переходить на трофический ресурс не доступный для другой популяции. Пусть 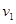 — численность первой популяции на новом трофическом ресурсе. Тогда модель (2) переходит в модель
— численность первой популяции на новом трофическом ресурсе. Тогда модель (2) переходит в модель
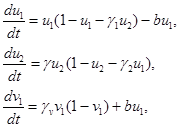 (5)
(5)
в которой 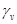 — постоянная, а
— постоянная, а 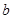 — скорость перехода особей первой популяции на новый трофический ресурс.
— скорость перехода особей первой популяции на новый трофический ресурс.
Как следует из анализа системы уравнений (2) при 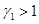 и
и 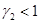 первая популяция в модели (2) погибает. При значениях
первая популяция в модели (2) погибает. При значениях 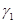 и
и 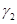 , удовлетворяющих этим неравенствам, стационарная точка системы уравнений (5)
, удовлетворяющих этим неравенствам, стационарная точка системы уравнений (5)
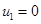 ,
, 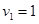 ,
, 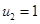
будет устойчивой, поскольку все собственные значения
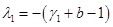 ,
, 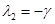 ,
, 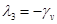
матрица Якоби правой части уравнений (5) в этой стационарной точке будут отрицательными. Это соответствует случаю полному переходу первой популяции на новый трофический ресурс.
При одновременном выполнении неравенств 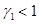 и
и 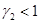 система уравнений может иметь нетривиальную стационарную точку
система уравнений может иметь нетривиальную стационарную точку
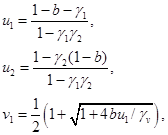
если выполняется неравенство 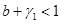 . При этом собственные значения матрицы Якоби правой части уравнений (5) являющиеся корнями уравнения
. При этом собственные значения матрицы Якоби правой части уравнений (5) являющиеся корнями уравнения
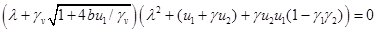 ,
,
будут иметь отрицательные вещественные части. То есть в случае реализации эта стационарная точка будет устойчивой.
Таким образом, в рамках подходов, применяемых в математической популяционной биологи при разработке математических моделей [4, 10], можно предложить математические модели «ухода» от конкуренции, обусловленным изменением «метаболизма» особей («пассивный уход» или «активный уход») или переходом особей на иной трофический ресурс. Влияние на эволюцию конкурирующих популяций могут оказывать различные факторы, с учетом которых можно строить и другие модели «ухода» от конкуренции. Это антропогенное воздействие, климатические условия, агрессивная внешняя среда, резкое изменение метаболизма особей, недостаток или избыток жизненно необходимых веществ [10, 20, 24, 36, 51, 52]. Математические модели конкуренции можно разрабатывать на основе моделей, описывающих другие системы взаимоотношений биологических популяций (например, хищник-жертва, симбиоз) [4, 10, 17, 23, 42–44, 50, 55]. Для учета пространственного распределения популяций можно использовать методы механики сплошных сред, находящихся под внешним воздействием, с учетом происходящих в среде «химических реакций» [18, 26, 27, 39, 40, 45, 46, 49, 58–60, 69–71, 89, 91, 95, 96]. На конкуренцию в системе экономических взаимоотношений могут влиять: выбор оптимальной стратегии предприятия [5, 12, 19, 25], умение принимать решения в условия неполноты информации [9, 11, 34, 64], рациональный ответ на внешнее воздействие [21], переход от конкуренции к партнерству [35, 54], уменьшение внутренних потерь за счет формирования «грамотного» персонала [13, 15, 50, 55, 62, 63, 76, 81]. Учет большего числа факторов в математических моделях приведет и к увеличению искомых функций, для нахождения которых необходимы и соответствующие методы решения математических задач [1, 29, 49, 64, 75].
Заключение. Рассмотренные математические модели эволюционных изменений во взаимоотношениях между конкурирующими популяциями объясняют возможные механизмы «ухода» от конкуренции либо путем изменения внутреннего метаболизма отдельных особей, либо постепенным уходом части популяции на новую «территорию». Наряду с этим возможно совместное существование нескольких популяций в условиях «жесткой» конкуренции, если она является «сезонной».
Литература:
1. Аббасов М. Э. О. Условия экстремума в терминах несобственных экзостеров∗) // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2011. — № 2. — С. 3–8.
2. Абдулина К. А., Старков В. Н. Квазистационарный подход в исследовании распространения насекомых в лесной системе // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2015. — № 1. — С. 5–15.
3. Александров А. Ю., Платонов А. В. О предельной ограниченности и перманентности решений одного класса дискретных моделей динамики популяций с переключениями // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2014. — № 1. — С. 5–16.
4. Базыкин А. Д. Нелинейная динамика взаимодействующих популяций. Москва-Ижевск: Институт компьютерных технологий, 2003. — 368 с.
5. Балакирева А. Е., Костина В. В., Меркушова Н. И. Интеграция классических и современных методик разработки конкурентной стратегии организации с целью повышения конкурентоспособности предприятия // Молодой ученый. — 2014. — № 2 (61). — С. 405–412.
6. Балыкина Ю. Е., Колпак Е. П. Математические модели функционирования фолликула щитовидной железы // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2013. — № 3. — С. 20–31.
7. Балыкина Ю. Е., Колпак Е. П. Модель роста фолликулярной клетки щитовидной железы / В сборнике: Современные методы прикладной математики, теории управления и компьютерных технологий (ПМТУКТ-2013) сборник трудов VI международной конференции. 2013. — С. 31–32.
8. Балыкина Ю. Е., Колпак Е. П. Точечная однокамерная модель функционирования фолликула щитовидной железы / В сборнике: Синергетика в общественных и естественных науках: девятые Курдюмовские чтения материалы Международной междисциплинарной научной конференции с элементами научной школы для молодежи. редкол.: Лапина Г. П. (отв. ред.) и др.. Тверь, 2013. — С. 157–158.
9. Басков О. В. Критерий непротиворечивости «квантов» информации о нечетком отношении предпочтения лица, принимающего решения // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2014. — № 2. — С. 12–18.
10. Бигон М., Харпер Дж., Таунсенд К. Экология. Особи, популяции и сообщества: в 2-х т. Т. 2. М.: Мир, 1989. — 477 с.
11. Буре А. В. Конкурентное прогнозирование в случае несобственного распределения вероятностей // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2014. — № 2. — С. 19–26.
12. Буре А. В. Об одной теоретико-игровой модели тендера // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2015. — № 1. — С. 25–32.
13. Буре В. М., Екимов А. В., Свиркин М. В. Имитационная модель формирования профиля мнений внутри коллектива // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2014. — № 3. — С. 93–98.
14. Валиотти Н. А. Нейросетевая модель для дифференцированной оценки влияния одновременных внешних событий в сфере розничной торговли // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2014. — № 2. — С. 111–119.
15. Вольтерра В. Математическая теория борьбы за существование. Москва-Ижевск:, Институт компьютерных технологий, 2004. — 288 с.
16. Гасратова Н. А., Бойцов Д. С., Габриелян Л. А., Тюганова Т. М. Математическая модель иммунного ответа организма млекопитающих на поражение кожи ожогом // Молодой ученый. — 2014. — № 12 (71). — С. 1–7.
17. Гасратова Н. А., Столбовая М. В., Бойцов Д. С., Степанова Д. С. Математическая модель хищник-жертва на линейном ареале // Молодой ученый. — 2014. — № 11. — С. 1–10.
18. Гасратова Н. А. Решение некоторых классических пространственных задач теории упругости в напряжениях // Молодой ученый. — 2014. — № 3 (62). — С. 1–6.
19. Гасратова Н. А., Гасратов М. Г. Сетевая модель управления запасами для случая количественной конкуренции // Сибирский журнал индустриальной математики. — 2015. — Т. 18. — № 1. — С. 14–27.
20. Гасратова Н. А., Столбовая М. В., Неверова Е. Г., Бербер А. С. Математическая модель «ресурс-потребитель» // Молодой ученый. — 2014. — № 10 (69). — С. 5–14.
21. Герасимчук З. В., Билык О. С. Анализ эколого-экономических конкурентных преимуществ регионов Украины // Молодой ученый. — 2013. — № 10. — С. 298–300.
22. Гиляров А. М. В поисках универсальных закономерностей организации сообществ: прогресс на пути нейтрализма // Журнал общей биологии. — 2010. — Т. 71. — № 5. — С. 386–401.
23. Горбунова Е. А., Колпак Е. А. Математические модели одиночной популяции // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2012. — № 4. — С. 18–30.
24. Горбунова М. В., Колпак Е. П., Крицкая А. В. Математическая модель антропогенного воздействия на одиночную популяцию / В сборнике: Синергетика в общественных и естественных науках: девятые Курдюмовские чтения материалы Международной междисциплинарной научной конференции с элементами научной школы для молодежи. редкол.: Лапина Г. П. (отв. ред.) и др. Тверь, 2013. — С. 165.
25. Гравшина И. Н. Конкурентная стратегия в системе управления конкурентоспособностью предприятия // Молодой ученый. — 2013. — № 6. — С. 296–298.
26. Даль Ю. М., Пронина Ю. Г. Деформация шаровой поры в нелинейно-упругом теле // Известия Российской академии наук. Серия физическая. — 2006. — Т. 70. — № 9. — С. 1341–1343.
27. Даль Ю. М., Пронина Ю. Г. Сосредоточенные силы и моменты у границы упругой полуплоскости // Известия Российской академии наук. Механика твердого тела. — 1998. — № 5. — С. 78.
28. Дегтярева А. В. Роль рекламы в новой экономике // Молодой ученый. — 2014. — № 20. — С. 257–261.
29. Жук В. В., Тумка О. А., Козлов Н. А. О константах в неравенствах типа Джексона для наилучших приближений периодических дифференцируемых функций // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2015. — № 1. — С. 33–41.
30. Жукова И. В., Колпак Е. П. Математическая модель солидной опухоли // Естественные и математические науки в современном мире. — 2013. — № 13. — С. 18–25.
31. Жукова И. В., Колпак Е. П. Математические модели злокачественной опухоли // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2014. — № 3. — С. 5–18.
32. Казарова А. Я. Формирование рыночных механизмов функционирования жилищно-коммунального комплекса // Молодой ученый. — 2013. — № 12 (59). — С. 312–314.
33. Капранова Н. Н. Современное предприятие в конкурентной среде // Молодой ученый. — 2014. — № 21 (80). — С. 328–332.
34. Карелин В. В Один подход к задаче оценки параметров динамической системы в условиях неопределенности // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2012. — № 4. — С. 31–36.
35. Колабутин Н. В. Двухуровневая кооперация в дифференциальной игре технологического альянса // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2015. — № 1. — С. 42–63.
36. Колесин И. Д., Старков В. Н., Гасратова Н. А. Одиночная популяция под антропогенным давлением // Журнал научных публикаций аспирантов и докторантов. — 2014. — № 6 (96). — С. 226–232.
37. Колобов А. Н. Численно-аналитическое исследование модели роста дерева в условиях конкуренции за свет // Математическая биология и биоинформатика. — 2012. — Т. 7. — № 1. — С. 125–138.
38. Колокольцов В. Н., Малафеев О. А. Динамические конкурентные системы многоагентного взаимодействия и их асимптотическое поведение (часть I) // Вестник гражданских инженеров. — 2010 — № 4 — С. 144–153.
39. Колпак Е. П. Устойчивость и закритические состояния безмоментных оболочек при больших деформациях // диссертация на соискание ученой степени доктора физико-математических наук / Санкт-Петербург, 2000.
40. Колпак Е. П. Введение в механику сплошных сред учебное пособие / Е. П. Колпак; С.-Петерб. гос. ун-т. СПб. 2004.
41. Колпак Е. П., Балыкина Ю. Е., Котина Е. Д., Жукова И. В. Математическая модель нарушений функционирования щитовидной железы // Молодой ученый. — 2014. — № 2 (61). — С. 19–24.
42. Колпак Е. П., Бронникова А. И., Полежаев В. Ю. Математическая модель стачечного движения в России в начале XX века // Молодой учёный. — 2015. — № 3 (83). — С. 4–15.
43. Колпак Е. П., Габриелян Л. А., Бронникова А. И., Крылова В. А. О математических моделях симбиоза // Молодой ученый. — 2015. — № 4 (84). — С. 6–14.
44. Колпак Е. П., Горбунова Е. А., Балыкина Ю. Е., Гасратова Н. А. Математическая модель одиночной популяции на билокальном ареале // Молодой ученый. — 2014. — № 1. — С. 28–33.
45. Колпак Е. П., Горбунова Е. А., Жукова И. В. Математическая модель популяционной волны // Естественные и математические науки в современном мире. — 2014. — № 16. — С. 25–41.
46. Колпак Е. П., Горбунова Е. А., Столбовая М. В., Балыкина Ю. Е. Математическая модель логистической популяции на линейном ареале // Молодой ученый. — 2014. — № 3 (62). — С. 6–14.
47. Колпак Е. П., Горыня Е. В., Крылова В. А., Полежаев Д. Ю. Математическая модель конкуренции двух популяций на линейном ареале // Молодой ученый. — 2014. — № 12 (71). — С. 12–22.
48. Колпак Е. П., Горыня Е. В., Полежаев В. Ю. Математическая модель конкуренции двух популяций (линейный ареал) / В сборнике: Современные методы прикладной математики, теории управления и компьютерных технологий (ПМТУКТ-2014) сборник трудов VII Международной конференции. Воронеж, 2014. С. 206–209.
49. Колпак Е. П., Жукова И. В., Степанова Д. С., Крицкая А. В. О численных методах решения эволюционных уравнений на примере математической модели «хищник-жертва» // Молодой ученый. — 2014. — № 4. — С. 20–30.
50. Колпак Е. П., Селицкая Е. А., Габриелян Л. А. Математическая модель коррупции в системе «власть-общество» // Молодой ученый. — 2015. — № 10 (90). — С. 9–16.
51. Колпак Е. П., Столбовая М. В. Математическая модель кинетики роста растений // Журнал научных публикаций аспирантов и докторантов. — 2013. — № 12 (90). — С. 230–232.
52. Колпак Е. П., Столбовая М. В. Математическая модель роста растений / В сборнике: Синергетика в общественных и естественных науках: девятые Курдюмовские чтения материалы Международной междисциплинарной научной конференции с элементами научной школы для молодежи. редкол.: Лапина Г. П. (отв. ред.) и др. Тверь, 2013. С. 186.
53. Кондратов М. В. Формирование и развитие теории конкуренции // Молодой ученый. — 2010. — № 6. — С. 146–149.
54. Кощеева П. П. Россия и НАТО: партнерство или конкуренция? // Молодой ученый. — 2012. — № 5. — С. 354–356.
55. Крылова В. А., Колпак Е. П., Сыромолотова К. И., Воротова Т. А. Математические модели формирования спортивных групп // Молодой учёный. — 2015. — № 8 (88). — C. 10–19.
56. Кузнецова Е. А. Влияние развития малого и среднего предпринимательства на развитие конкуренции // Молодой ученый. — 2012. — № 2. — С. 126–128.
57. Малков С. Ю., Кирилюк И. Л. Моделирование динамики конкурирующих сообществ: варианты взаимодействия // Информационные войны. — 2013. — № 2 (26). — С. 49–56.
58. Мальков В. М., Малькова Ю. В. Анализ сингулярности напряжений в нелинейной задаче фламана для некоторых моделей материала // Прикладная математика и механика. — 2008. — Т. 72. — № 4. С. 652–660.
59. Мальков В. М., Малькова Ю. В. Нелинейная задача Фламана для материала Бартенева-Хазановича // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2005. — № 1–2. — С. 49–55.
60. Мальков В. М., Малькова Ю. В. Плоские задачи о сосредоточенных силах для полулинейного материала // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2013. — № 3. — С. 83–96.
61. Миндлин Ю. Б., Колпак Е. П., Балыкина Ю. Е. Проблемы использования кластеров в Российской Федерации // Вестник НГУЭУ. — 2014. — № 1. — С. 22–32.
62. Молчанова Е. Н. Конкурентоспособность персонала как один из ключевых факторов конкурентоспособности организации // Молодой ученый. — 2014. — № 6 (65). — С. 458–460.
63. Морозова Н. С. Виртуальные формации и виртуальные лидеры в задаче о движении строем группы роботов // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2015. — № 1. — С. 135–149.
64. Олемской И. В., Фирюлина О. С. Алгоритм поиска наибольшего независимого множества // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2014. — № 1. — С. 79–89.
65. Орлова Е. В., Ульмасова И. С. Методы ценообразования и их использование на высоко конкурентном рынке // Молодой ученый. — 2014. — № 3 (62). — С. 495–497.
66. Полякова Л. Н., Карелин В. В., Буре В. М., Хитров Г. М. Точные штрафные функции в задаче управления одной системой массового обслуживания // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2015. — № 1. — С. 75–82.
67. Попова И. Ю. Информационная составляющая упаковки, как одна из составляющих конкурентных преимуществ предприятий индустрии питания // Молодой ученый. — 2015. — № 2. — С. 297–300.
68. Поспелов И. Г., Радионов С. А. Динамика количества фирм в рамках концепции экономики разнообразия // Математическое моделирование. — 2014. — Т. 26. — № 2. — С. 65–80.
69. Пронина Ю. Г. Периодическая задача о точечных воздействиях в упругой полуплоскости с отверстиями // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2009. — № 3. — С. 118–128.
70. Пронина Ю. Г. Сосредоточенные силы и моменты в упругой полуплоскости с отверстием // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2009. — № 2. — С. 104–114.
71. Пронина Ю. Г. Центры расширения-сжатия в упругой полуплоскости // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2007. — № 2. — С. 140–149.
72. Решетько Н. И., Понявина М. Б., Абрамова К. В. Конкуренция в сетевой фирме // Молодой ученый. — 2014. — № 6–2 (65). — С. 49–52.
73. Российский статистический ежегодник. М.: Статистика России, 2013. — 717 с.
74. Сандомирская М. С. Цена внезапного раскрытия инсайдерской информации на фондовом рынке // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2014. — № 1. — С. 120–127.
75. Слупко К. А. Периодические дифференциально-разностные системы. алгоритм построения матрицы Ляпунова // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2015. — № 1. — С. 150–159.
76. Смирнова М. В., Колпак Е. П. Математическое моделирование снижения детской заболеваемости в России / В сборнике: Синергетика в общественных и естественных науках: девятые Курдюмовские чтения материалы Международной междисциплинарной научной конференции с элементами научной школы для молодежи. редкол.: Лапина Г. П. (отв. ред.) и др.. Тверь, 2013. — С. 222.
77. Суска А. А. Конкурентный потенциал как категория конкуренции и объект управления // Молодой ученый. — 2012. — № 12. — С. 277–279.
78. Ткаченко О. Н. Значение информационных технологий в формировании конкурентных преимуществ промышленных предприятий // Молодой ученый. — 2015. — № 6 (86). — С. 469–471.
79. Ульянченко А. В., Евчук Л. А. Роль информационных технологий в формировании конкурентных преимуществ сельскохозяйственных предприятий // Молодой ученый. — 2012. — № 8. — С. 146–149.
80. Файзрахманов И. М., Файзрахманова А. Л. Формирование ценностно-коммуникативной составляющей готовности будущих учителей к конкурентным отношениям // Молодой ученый. — 2013. — № 3. — С. 502–504.
81. Фирюлина О. С. Нахождение всех максимальных независимых множеств неориентированного графа // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2013. — № 1. — С. 63–69.
82. Харламов О. И., Булатов Б. Р. Особенности монополистической конкуренции // Молодой ученый. — 2014. — № 15–1. — С. 148–150
83. Цю Ш. Разработка системы управления конкурентной стратегией // Молодой ученый. — 2014. — № 21 (80). — С. 456–458.
84. Шестакова Т. П. Исследование одной математической модели конкуренции трех популяций // Инновации в науке. — 2012. — № 7. — С. 6–11.
85. Шоев А. Х. Некоторые аспекты конкурентной борьбы за ресурсы в мировой экономике // Молодой ученый. — 2014. — № 6 (65). — С. 532–534.
86. Шустов А. А. Роль инновационной деятельности в конкурентной борьбе предприятия // Молодой ученый. — 2013. — № 10. — С. 412–416.
87. Яковлева Ю. А. Роль конкуренции в рыночной экономике // Молодой ученый. — 2014. — № 3 (62). — С. 610–613.
88. Balykina Y. E., Kolpak E. P., Kotina E. D. Mathematical model of thyroid function // Middle East Journal of Scientific Research. — 2014. — Т. 19. — № 3. — С. 429–433.
89. Dal' Yu.M., Pronina Yu. G. On concentrated forces and moments in an elastic half-plane // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 1998. — № 1. — С. 57–60.
90. Hutchinson G. E. Homage to Santa Rosalia, or why are there so many kinds of animals? // American Naturalist. — 1959. — V. 93. — C. 145–159.
91. Kolpak E. P., Ivanov S. E. Mathematical and computer modeling vibration protection system with damper // Applied Mathematical Sciences. — 2015. — V. 9. — no. 78. — C. 3875–3885.
92. Mirrahimi S., Perthame B., Yuichiro Wakano J. Direct competition results from strong competition for limited resource // Journal of Mathematical Biology. — 2014. — V. 68. — 931–949.
93. Mozzherina E. An approach to improving the classification of the New York Times annotated corpus // Communications in Computer and Information Science. — 2013. — Т. 394. — С. 83–91.
94. Peresada V. P., Smirnov N. V. E., Smirnova T. E. Development control of a multicommodity economy based on the dynamical input-output model // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2014. — № 4. — С. 119–132.
95. Pronina Y. Analytical solution for the general mechanochemical corrosion of an ideal elastic-plastic thick-walled tube under pressure // International Journal of Solids and Structures. — 2013. — Т. 50. — № 22–23. — С. 3626–3633.
96. Pronina Y. G. Estimation of the life of an elastic tube under the action of a longitudinal force and pressure under uniform surface corrosion conditions // Russian metallurgy (Metally). — 2010. — Т. 2010. — № 4. — С. 361–364.
97. Sanling Yuan, Dongmei Xiao, Maoan Han Competition between plasmid-bearing and plasmid-free organisms in a chemostat with nutrient recycling and an inhibitor // Mathematical Biosciences. — 2006. — V. 202. — N 1. — P. 1–28.
98. Sze-Bi Hsu, Xiao-Qiang Zhao A Lotka–Volterra competition model with seasonal succession // Journal of Mathematical Biology. — 2012. — DOI 10.1007/s00285–011–0408–6.
99. Zhukova I. V., Kolpak E. P., Balykina Yu. E. Mathematical Model of Growing Tumor // Applied Mathematical Sciences. — V. 9. — 2014. N 30. — 1455–1466.







