Формулируется математическая модель иммунного ответа организма млекопитающего на поражении кожи ожогом. Модель представляет собой краевую задачу для системы четырех нелинейных дифференциальных уравнений в частных производных. Предлагается алгоритм численного решения нелинейной краевой задачи. Проведено исследование влияния различных параметров на поведение решений.
Ключевые слова: ожоги, краевые задачи, математическое моделирование.
Введение. Широкое использование на производстве и в быту электроэнергии, газа, различного рода горюче-смазочных материалов и химически активных веществ — приводит к увеличению ожогового травматизма [2, 6, 21, 38, 41]. В вооруженных конфликтах используются различного рода средства, вызывающие термическое и химическое поражение органов млекопитающих [43, 53]. По данным Всемирной организации здравоохранения, ожоги занимают третье место среди всех травм [50]. Лечение ожогов осуществляется различными лекарственными средствами (такими, как мази и гели) [32, 40], пересадкой донорской ткани на пораженные ожогами участки или покрытием пораженных участков выращенными из различных клеток «перфорированными» тканями [15, 17, 31, 33, 42, 52, 54, 57]. Что касается математического моделирования иммунного ответа организма на поражение ожогом и моделирования методов лечения, то публикации на эту тему в литературных источниках практически отсутствуют [5, 14]. Значительная часть работ относится к моделированию термического удара [58, 59, 61, 62].
Кожа защищает организм от механических, физических, и химических воздействий, препятствует проникновению в кровь вирусов, бактерий и грибов. Кожный покров не дает организму нарушать свою структуру, свою форму, свою внутреннюю среду. Термические, химические и другие ожоги поражают участки кожи и вызывают целый ряд патологических изменений в организме. Возникают иммунологические сдвиги в организме, развивается интоксикация, связанная с накоплением продуктов распада белков, токсических веществ, поступающих из обожженных тканей и обладающих антигенными свойствами. Создаются условия для возникновения самых разнообразных инфекционных осложнений. Пораженная поверхность, как правило, загрязнена различными микроорганизмами, проникающими через пораженные участки во внутреннюю среду организма. При поражении организма в результате внешнего воздействия иммунная система начинает бороться с чужеродными элементами, проникающими в организм [21, 38].
При построении математической модели иммунного ответа используются методы математической популяционной биологии [19, 26–30, 49] и математической физики [55, 56].
Модель иммунного ответа. Кожу можно разделить на две части: внешний слой, контактирующий с внешним миром, и внутренний слой. Слои разделены базальной мембраной. На мембране со стороны внешнего слоя расположены стволовые клетки, которые пролиферируют, когда необходимо заменить отмирающие клетки внешнего слоя. Часть этих клеток отрывается от базальной мембраны, созревает, и прекращает пролиферацию. Образовавшиеся из стволовых зрелые клетки верхнего слоя выталкиваются на поверхность кожи. По мере движения они выполняют свои функции по выработке белков и, достигнув поверхности кожи, прекращают выполнять свои функции.
При слабом ожоге поражается часть верхнего слоя, иммунная система организма воздействует на пораженный участок со стороны базальной мембраны, уничтожая некротическую ткань. Область, пораженная поверхностным ожогом, представляет собой тонкий слой некротической ткани. Иммунная система организма воздействует на его внутреннюю поверхность. Если линейные размеры пораженного участка кожи значительно больше по сравнению с толщиной некротической ткани, то в первом приближении можно считать, что реакция иммунной системы на некротическую ткань одинаковая в каждой точке внутренней поверхности ожогового слоя со стороны базальной мембраны. Потому в математической модели в первом приближении рассматривается одномерная (по толщине) модель иммунного ответа.
Верхний слой кожи, в котором находятся лимфоциты, пролиферирующие, эпителиальные и некротические клетки представляется в виде отрезка длиной 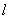 . Точка
. Точка 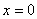 «соответствует» базальной мембране, а точка
«соответствует» базальной мембране, а точка 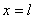 — внешней поверхности кожи. Пусть
— внешней поверхности кожи. Пусть 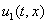 — линейная плотность пролиферирующих клеток,
— линейная плотность пролиферирующих клеток, 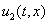 — линейная плотность эпителиальных клеток,
— линейная плотность эпителиальных клеток, 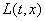 — линейная плотность лимфоцитов, уничтожающих некротическую ткань,
— линейная плотность лимфоцитов, уничтожающих некротическую ткань, 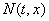 — линейная плотность некротических клеток. В точке
— линейная плотность некротических клеток. В точке 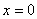 расположены пролиферирующие клетки концентрация
расположены пролиферирующие клетки концентрация 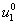 , которые за счет диффузии начинают распространяться вдоль отрезка. Созревание этих клеток (
, которые за счет диффузии начинают распространяться вдоль отрезка. Созревание этих клеток (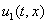 ) на отрезке сопровождается их превращением в эпителиальные клетки
) на отрезке сопровождается их превращением в эпителиальные клетки 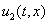 . Последние, выполняя свои функции, за счет диффузии перемещаются к точке
. Последние, выполняя свои функции, за счет диффузии перемещаются к точке 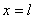 (внешнему слою кожи). В точке
(внешнему слою кожи). В точке 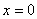 концентрация лимфоцитов поддерживается постоянной и равной
концентрация лимфоцитов поддерживается постоянной и равной 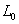 . При
. При 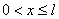 источники клеток
источники клеток 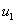 и
и 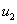 отсутствуют.
отсутствуют.
Некротические клетки 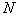 расположены в окрестности точки
расположены в окрестности точки 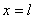 . При этом их общее количество, поскольку они «замещают» здоровые клетки, не должно превышать
. При этом их общее количество, поскольку они «замещают» здоровые клетки, не должно превышать 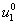 . В область залегания только некротических клеток клетки
. В область залегания только некротических клеток клетки 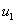 и
и 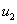 не проникают.
не проникают.
При введенных предположениях математическая модель ответа иммунной системы на наличие некротических клеток представляется системой дифференциальных уравнений
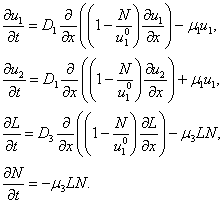 (1)
(1)
В этих уравнениях 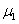 — константа, характеризующая скорость превращения клеток
— константа, характеризующая скорость превращения клеток 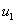 в клетки
в клетки 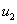 ,
, 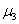 — константа, характеризующая скорость уничтожения некротических клеток лимфоцитами,
— константа, характеризующая скорость уничтожения некротических клеток лимфоцитами, 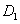 — параметр, характеризующий подвижность клеток
— параметр, характеризующий подвижность клеток 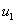 и
и 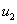 , а
, а 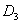 — лимфоцитов. Нелинейность проникновения клеток
— лимфоцитов. Нелинейность проникновения клеток 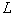 ,
, 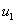 и
и 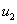 в область некротических клеток учтена множителем
в область некротических клеток учтена множителем 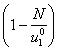 в первых трех уравнениях в (1).
в первых трех уравнениях в (1).
К уравнениям (1) добавляются граничные условия при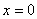
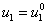 ,
, 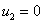 ,
, 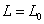 ,
, 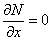 (2)
(2)
и при 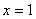
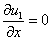 ,
, 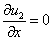 ,
, 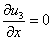 ,
, 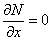 . (3)
. (3)
Эти граничные условия предполагают, что клетки 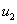 отсутствуют на границах отрезка, концентрация клеток
отсутствуют на границах отрезка, концентрация клеток 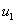 в точке
в точке 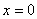 поддерживается постоянной (базальная мембрана не повреждена), а в точке
поддерживается постоянной (базальная мембрана не повреждена), а в точке 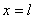 диффузионные потоки равны нули.
диффузионные потоки равны нули.
В качестве начальных условий принимаются следующие
при 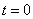 :
:
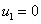 ,
, 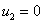 ,
, 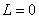 ,
, 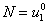 , если
, если 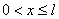 ,
,
и
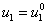 ,
, 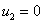 ,
, 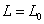 ,
, 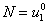 , если
, если 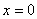 .
.
Здесь предполагается, что верхний слой ткани вплоть до базальной мембраны представляет собой некротическую ткань, а сама базальная мембрана не поражена.
Общее количество некротических клеток в момент времени 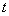 подсчитывается по формуле
подсчитывается по формуле
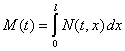 .
.
В отсутствие некротической ткани функция 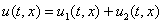 удовлетворяет линейному уравнению
удовлетворяет линейному уравнению
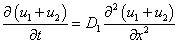 ,
,
решение которого со временем с учетом граничных условий (2) — (3) стремится к решению стационарного уравнения [55]: 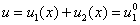 .
.
Функция 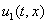 в стационарном случае удовлетворяет уравнению
в стационарном случае удовлетворяет уравнению
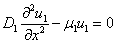 .
.
Решение этого уравнения, удовлетворяющее граничному условию при 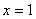 , представляется в виде неявной зависимости
, представляется в виде неявной зависимости 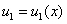 [1]:
[1]:
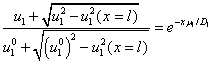 .
.
Значение 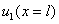 находится как корень уравнения
находится как корень уравнения
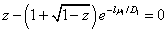 , (4)
, (4)
в котором 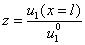 , имеющего решение при
, имеющего решение при 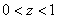 . Поверхности кожи пролиферирующие клетки не достигают. То есть в модели должно выполняться неравенство
. Поверхности кожи пролиферирующие клетки не достигают. То есть в модели должно выполняться неравенство 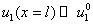 . Поэтому корень уравнения (4) должен быть близким к нулю. Это выполняется, если
. Поэтому корень уравнения (4) должен быть близким к нулю. Это выполняется, если 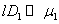 — диффузия клеток должна быть медленной, по сравнению со скоростью пролиферации (или большая часть пролиферирующие клеток должна находиться в окрестности базальной мембраны).
— диффузия клеток должна быть медленной, по сравнению со скоростью пролиферации (или большая часть пролиферирующие клеток должна находиться в окрестности базальной мембраны).
Численное решение. Построение численного решения системы уравнений (1) осуществлялось с применением сеточных методов. Дискретизация уравнений (1) осуществлялась по пространственной и временной переменным [29, 55]. По пространственной переменной с шагом 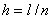 (
(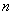 — число отрезков разбиения промежутка
— число отрезков разбиения промежутка 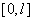 ) и временной переменной с шагом
) и временной переменной с шагом 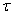 . Дифференциальные уравнения в (1) аппроксимировались конечными разностями. Во внутренних точка промежутка
. Дифференциальные уравнения в (1) аппроксимировались конечными разностями. Во внутренних точка промежутка 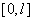 (
(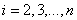 )
)
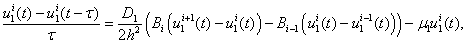
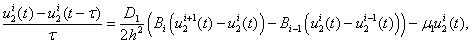
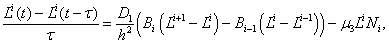 (5)
(5)
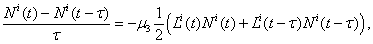
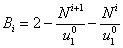 ,
,
и на границах
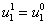 ,
, 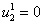 ,
, 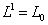 ,
, 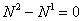
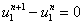 ,
, 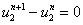 ,
, 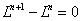 ,
, 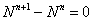 .
.
Система уравнений (5) на каждом временном слое решалась итерационными методами. Требуемая точность (не более 1 % в максимальных относительных отклонениях на двух соседних итерациях) достигалась при 3–5 итерациях. Результаты решения системы уравнений для 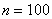 и
и 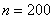 при шаге интегрирования по временной переменной, выбираемом из условия
при шаге интегрирования по временной переменной, выбираемом из условия 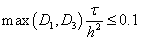 , отличались не более чем на 1 %. Некоторые из результатов решения уравнений (5) представлены на рис. 1–2 (
, отличались не более чем на 1 %. Некоторые из результатов решения уравнений (5) представлены на рис. 1–2 (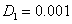 ,
, 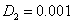 ,
, 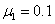 ,
, 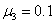 ,
, 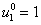 ,
, 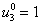 ,
, 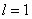 ). На рис. 1 показано изменение функций
). На рис. 1 показано изменение функций 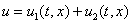 ,
, 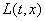 и
и 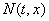 вдоль координаты в момент времени
вдоль координаты в момент времени 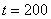 . На рис. 2 — изменение общего количества некротических клеток
. На рис. 2 — изменение общего количества некротических клеток 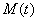 во времени при различных значениях параметра
во времени при различных значениях параметра 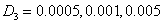 .
.
Как следует из полученных результатов в рамках предложенной модели иммунного ответа организма для ускорения уничтожения некротических клеток необходимо повышать подвижность лимфоцитов.
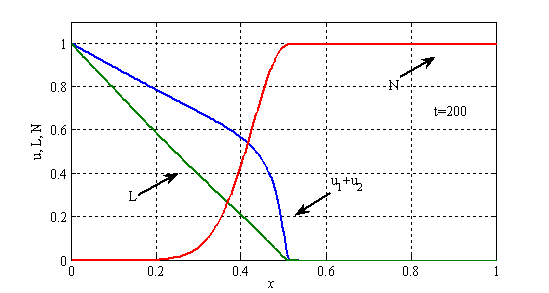
Рис. 1. Изменение функций 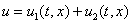 ,
, 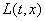 и
и 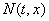 вдоль координаты в момент времени
вдоль координаты в момент времени 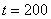
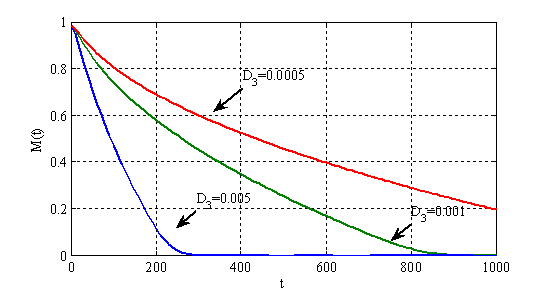
Рис. 2. Изменение функции 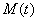 во времени при различных значениях параметра
во времени при различных значениях параметра 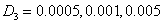
При ожогах изменяются механические свойства кожи и ее форма [3, 4]. Учет в математических моделях этих эффектов можно осуществлять на основе законов механики с учетом биохимических реакций, происходящих в среде [1, 23, 44–49, 55, 60, 63, 64]. В этом случае можно на основе математического моделирования спланировать лечение с наименьшими искажениями формы кожи после восстановления ее функций [2, 18, 25, 51]. С другой стороны подключение аппарата механики сплошных сред позволит разрабатывать модели поражения как внешних, так и внутренних органов организма различной геометрической формы с нелинейными механическими свойствами тканей [7–9, 13, 24, 34–37, 56]. Для расчета экономических и временных затрат на лечение ожоговой болезни можно использовать методы математической экономики [10–12, 20, 22, 39]. Это позволит спланировать наиболее рациональный вариант лечения в рамках имеющихся материальных и временных ресурсов [16].
Работа частично поддержана грантом РФФИ 14–06–00326.
Литература:
- Балыкина Ю. Е., Колпак Е. П. Математические модели функционирования фолликула щитовидной железы // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2013. — № 3. — С. 20–31.
- Буланкина И. А. Изменения морфологических характеристик и биомеханических свойств структур кожи при термическом ожоге III, IV степени // Сибирский медицинский журнал (г. Иркутск). — 2011. — Т. 106. — № 7. — С. 23–26.
- Буланкина И. А. Изменения напряженно-деформированных состояний структур кожи при термическом ожоге без признаков некроза (I, II степени) // Сибирский медицинский журнал (г. Иркутск). — 2011. — Т. 103. — № 4. — С. 95–98.
- Буланкина И. А., Лебединский В. Ю., Изатулин В. Г. Изменения напряженно-деформированных состояний структур кожи при термическом ожоге с признаками некроза (III, IV степени) // Сибирский медицинский журнал (г. Иркутск). — 2010. — Т. 96. — № 5. — С. 57–59.
- Викторов А. А., Холоднов В. А., Гладких В. Д., Алехнович А. В. Математическая модель влияния окружающей среды на старение живых систем // Успехи геронтологии. — 2013. — Т. 26. — № 1. — С. 52–57.
- Гамаюнов Б. Н. Солнечные ожоги — причины, профилактика и способы лечения // Фарматека. — 2013. — № 10 (263). — С. 63–65.
- Гасратова Н. А. Напряженно-деформированное состояние упругого пространства со сферическим жестким включением // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2009. — № 1. — С. 14–18.
- Гасратова Н. А., Столбовая М. В., Неверова Е. Г., Бербер А, С Математическая модель «ресурс-потребитель» // Молодой ученый. — 2014. — № 10 (69). — С. 5–14.
- Гасратова Н. А., Шамина В. А. Решение в напряжениях линейной осесимметричной задачи для сферы и упругого пространства со сферической полостью // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2008. — № 2. — С. 122–128.
- Гордеев Д. A., Малафеев О. А. Титова Н. Д. Стохастическая модель принятия решения о выводе на рынок инновационного продукта // Вестник гражданских инженеров — 2011 — № 2. — С. 161–166.
- Григорьева К. В., Малафеев О. А. Динамический процесс кооперативного взаимодействия в многокритериальной (многоагентной) задаче почтальона // Вестник гражданских инженеров — 2011 — № 1. — С. 150–156.
- Григорьева К. В., Иванов А. С., Малафеев О. А. Статическая коалиционная модель инвестирования инновационных проектов // Экономическое возрождение России — 2011 — № 4. — С. 90–98.
- Даль Ю. М., Пронина Ю. Г. Деформация шаровой поры в нелинейно-упругом теле // Известия Российской академии наук. Серия физическая. — 2006. — Т. 70. — № 9. — С. 1341–1343.
- Домогатская А. С., Домогатский С. П., Руге Э. К. Обработка протеолитическими ферментами поверхности ожоговых ран: математическое описание кинетики лизиса // Биофизика. — 2003. — Т. 48. — Вып.5. — С. 911–917.
- Дрозд В. А., Мартыненко Е. Е., Митряшов К. В., Гиря О. Ю., Маломан Н. В. Применение наночастиц в лечении ожогов кожи // Успехи современного естествознания. — 2013. — № 8. — С. 44–45.
- Дроздова И. В. Моделирование процессов реконструкции жилищно-коммунального хозяйства мегаполиса в условиях конкурентной среды: монография / И. В. Дроздова, О. А. Малафеев, Г. Д. Дроздов — М-во образования и науки Российской Федерации, Федеральное агентство по образованию, Санкт-Петербургский гос. ун-т сервиса и экономики — Санкт-Петербург, 2008.
- Еремин И. И., Зорин В. Л., Поляков А. В., Черкасов В. Р., Зорина А. И. Клеточные технологии в терапии ожогов // Патологическая физиология и экспериментальная терапия. — 2011. — № 4. — С. 75–81.
- Жукова И. В., Колпак Е. П. Математическая модель солидной опухоли // Естественные и математические науки в современном мире. — 2013. — № 13. — С. 18–25.
- Жукова И. В., Колпак Е. П. Математические модели злокачественной опухоли // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2014. — № 3. — С. 5–18.
- Занина И. А., Раздорская И. М., Чембарцева И. В. Прогнозирование затрат на антибактериальные препараты для лечения ожогов у детей // Фармация. — 2009. — № 4. — С. 25–26.
- Кожевников П. В. Общая дерматология. Л.: Медицина, 1970. — 295с.
- Колокольцов В. Н., Малафеев О. А. Динамические конкурентные системы многоагентного взаимодействия и их асимптотическое поведение (часть I) // Вестник гражданских инженеров — 2010 — № 4 — С. 144–153.
- Колпак Е. П. Введение в механику сплошных сред учебное пособие / Е. П. Колпак; С.-Петерб. гос. ун-т. СПб. 2004.
- Колпак Е. П. Устойчивость и закритические состояния безмоментных оболочек при больших деформациях // диссертация на соискание ученой степени доктора физико-математических наук / Санкт-Петербург, 2000.
- Колпак Е. П., Балыкина Ю. Е., Котина Е. Д., Жукова И. В. Математическая модель нарушений функционирования щитовидной железы // Молодой Ученый. — 2014. — № 2(61). — С. 19–24.
- Колпак Е. П., Горбунова Е. А., Балыкина Ю. Е., Гасратова Н. А. Математическая модель одиночной популяции на билокальном ареале // Молодой ученый. — 2014. — № 1 (6). — С. 28–33.
- Колпак Е. П., Горбунова Е. А., Жукова И. В. Математическая модель популяционной волны // Естественные и математические науки в современном мире. — 2014. — № 16. — С. 25–41.
- Колпак Е. П., Горбунова Е. А., Столбовая М. В., Балыкина Ю. Е Математическая модель логистической популяции на линейном ареале // Молодой ученый. — 2014. — № 3 (62). — С. 6–14.
- Колпак Е. П., Жукова И. В., Степанова Д. С., Крицкая А. В. О численных методах решения эволюционных уравнений на примере математической модели «хищник-жертва» // Молодой ученый. — 2014. — № 4. — С. 20–30.
- Колпак Е. П., Столбовая М. В. Математическая модель кинетики роста растений // Журнал научных публикаций аспирантов и докторантов. — 2013. — № 12 (90). — С. 230–232.
- Королёва Т. А. Клеточные технологии в лечении детей с глубокими ожогами кожи (обзор литературы) // Российский вестник детской хирургии, анестезиологии и реаниматологии. — 2013. — Т. III. — № 3. — С. 35–42.
- Крылов П. К., Козулин И. Д. Применение гелей на основе 2-аллилоксиэтанола в процессе местного лечения ожогов // Скорая медицинская помощь. — 2014. — Т. 15. — № 1. — С. 59–63.
- Ледовской С. Н., Лазаренко В. А., Бурда Ю. Е. Сравнительный экономический анализ получения первичной культуры фибробластов различной степени зрелости для лечения ожогов // Курский научно-практический вестник Человек и его здоровье. — 2010. — № 1. — С. — 111–116.
- Мальков В. М., Малькова Ю. В. Исследование нелинейной задачи Фламана // Известия Российской академии наук. Механика твердого тела. — 2006. — № 5. — С. 68–78.
- Мальков В. М., Малькова Ю. В. Нелинейная задача Фламана для несжимаемого материала // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2004. — № 4. — С. 73–82.
- Мальков В. М., Малькова Ю. В., Иванов В. А. Бесконечная плоскость с круговым включением, имеющим отслоение на части границы // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2009. — № 4. — С. 152–165.
- Мальков В. М., Малькова Ю. В.Плоская задача нелинейной упругости для гармонического материала // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2008. — № 3. — С. 114–126.
- Матвеев С. Б., Смирнов С. В., Тазина Е. В., Шахламов М. В., Годков М. А., Борисов В. С. Динамика эндогенной интоксикации у пациентов с обширными ожогами // Клиническая лабораторная диагностика. — 2013. — № 2. — С. 10–12.
39. Миндлин Ю. Б., Колпак Е. П., Балыкина Ю. Е Проблемы использования кластеров в Российской Федерации // Вестник НГУЭУ. — 2014. — № 1. — С. 22–32.
- Миненко Н. А., Панов П. Б. Профилактика химических ожогов кожи, вызванных действием агрессивных жидкостей // Медико-биологические и социально-психологические проблемы безопасности в чрезвычайных ситуациях. — 2012. — № 1. — С. 16–21.
- Михайлов И. Н. Структура и функция эпидермиса. М.: Медицина, 1979. — 238 с.
- Никитенко В. И., Павловичев С. А., Полякова В. С., Копылов В. А., Гнедой С. Н., Миханов В. А., Никитенко И. Е. Использование факторов роста фибробластов для лечения ран и ожогов // Хирургия. Журнал им. Н. И. Пирогова. — 2012. — № 12. — С. 72–76.
- Правдивцев В. Л. Тайные технологии. Биосферное и геосферное оружие / В. Л. Правдивцев. — М.: Бином. Лаборатория знаний, 2012. — 335 с
- Пронина Ю. Г. Оценка долговечности упpугой тpубы под действием пpодольной силы и давления в условиях pавномеpной поверхностной коppозии // Деформация и разрушение материалов. — 2009. — № 2. — С. 41–45.
- Пронина Ю. Г. Механохимическая коррозия полого цилиндра из идеального упругопластического материала под действием постоянного давления // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2006. — № 3. — С. 121–130.
- Пронина Ю. Г. Периодическая задача о точечных воздействиях в упругой полуплоскости с отверстиями // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2009. — № 3. — С. 118–128.
- Пронина Ю. Г. Сосредоточенные силы и моменты в упругой полуплоскости с отверстием // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2009. — № 2. — С. 104–114.
- Пронина Ю. Г. Центры расширения-сжатия в упругой полуплоскости // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2007. — № 2. — С. 140–149.
- Ризниченко Г. Ю., Рубин А. Б. Биофизическая динамика продукционных процессов. Москва — Ижевск: Институт компьютерных технологий, 2004. — 464 с.
- Российский статистический ежегодник. 2005: Росстат. М., 2006. — 819с.
- Рыбаков А. А., Ершов А. В., Долгих В. Т. Оптимизация лечения больных с термическими ожогами II-III степени // Общая реаниматология. — 2009. — Т. V. — № 5. — С. 45–48.
- Салахиддинов К. З., Алексеев А. А. Роль биосинтетических покрытий в лечении поверхностных ожогов II-III степени // Казанский медицинский журнал. — 2013. — Т. 94. — № 4. — С. 487–491.
- Соколов В. А., Адмакин А. Л., Петрачков С. А., Степаненко А. А., Камаев В. В. Ожоги после террористических актов и чрезвычайных ситуаций мирного времени // Медико-биологические и социально-психологические проблемы безопасности в чрезвычайных ситуациях. — 2014. — № 2. — С. 24–32.
- Стручков А. А., Анфимов П. Е., Кулакова К. В., Бугров С. Н. Применение раневого покрытия «биотекст» для местного лечения ожогов // Вопросы травматологии и ортопедии. — 2012. — № 2. — С. 16–17.
- Тихонов А. Н., Самарский А. А. Уравнение математической физики. М.: Наука, 1972. 735 с.
- Черных К. Ф., Кабриц С. А., Колпак Е. П., Слепнева Л. В. Точные решения краевых задач нелинейной теории упругости // отчет о НИР № 96–01–00739 (Российский фонд фундаментальных исследований).
- Шубина В. С., Шаталин Ю. В. Регенерация кожи после химического ожога в присутствии препаратов на основе производных таксифолина // Клеточные технологии в биологии и медицине. — 2012. — № 3. — С. 160–166.
- Jiang S. C., Ma N., Li H. J., Zhang X. X. Effects of thermal properties and geometrical dimensions on skin burn injuries // Burns. — 2002. — V. 28. — P. 713–717.
- Mercer G. N., Sidhu Y. S. Modeling thermal burns due to airbag deployment // Burns. — 2005. V. 31. P. 977–980.
- Murray D. D. Mathematical biology. N. Y. Springer. 2002. — 551 p.
- Museux N., Perez L., AutriqueL., Agay D. Skin burns after laser exposure: Histological analysis and predictive simulation // Burns. — 2012. — V. 38. — P. 658–667.
- Ng E. Y. K., Tan H. M., Ooi E. H. Boundary element method with bioheat equation for skin burn injury // Burns. — 2009. — V. 35. — P. 987–997.
- Pronina Y. Analytical solution for the general mechanochemical corrosion of an ideal elastic-plastic thick-walled tube under pressure // International Journal of Solids and Structures. — 2013. — Т. 50. — № 22–23. — С. 3626–3633.
- Pronina Y. G. Estimation of the life of an elastic tube under the action of a longitudinal force and pressure under uniform surface corrosion conditions // Russian metallurgy (Metally). — 2010. — Т. 2010. — № 4. –С. 361–364.







