В статье рассмотрены методы решения учебных вариационных задач на ПЭВМ. Предложены 3 компьютерных программы, проанализированы задачи на расчет формы: 1) неоднородной нити в поле тяжести (с подвешенными к ней грузами и без них); 2) упругой пластины в поле тяжести; 3) мыльной пленки, натянутой между двумя кольцами; 4) капли, лежащей на горизонтальной поверхности.
Ключевые слова: компьютерное моделирование, вариационные задачи, программирование.
Многие проблемы сводятся к основной задаче вариационного исчисления: найти такую функцию, для которой некоторый функционал принимает экстремальное значение, то есть его вариация равна 0. Например, задача о форме свободной поверхности жидкости, мыльной пленки; задача о форме неоднородной нити или пластины в поле тяжести; задача об оптимальном распределении ресурсов при планировании работы предприятия; задача о распространении света в оптически неоднородной среде и т. д. Эффективным методом численного решения вариационных задач является метод локальных вариаций [1–4]. Рассмотрим решение нескольких вариационных задач на ПЭВМ.
Задача 1. Имеется неоднородная нить или цепь. Определите форму, которую она примет в однородном поле тяжести, если ее концы закрепить в фиксированных точках. Решение:Нить примет форму, при которой ее потенциальная энергия минимальна. Мысленно заменим нить совокупностью материальных точек с массами 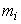 , которые связаны друг с другом пружинками жесткостью
, которые связаны друг с другом пружинками жесткостью 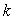 и длиной
и длиной  . Расстояние между соседними частицами и потенциальная энергия всей системы определяются уравнениями:
. Расстояние между соседними частицами и потенциальная энергия всей системы определяются уравнениями:
 ,
, 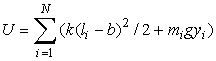 .
.
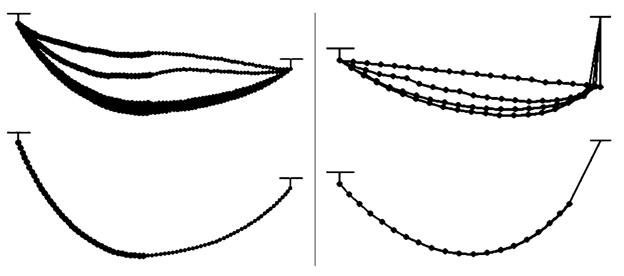
Рис. 1. Результаты вычисления формы неоднородной нити в поле тяжести.
Допустим, правый конец нити привязан математическому маятнику длиной 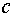 и массой
и массой 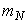 . Заменим нить маятника пружиной с большой жесткостью
. Заменим нить маятника пружиной с большой жесткостью 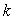 и длиной
и длиной 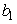 , тогда к потенциальной энергии системы следует прибавить
, тогда к потенциальной энергии системы следует прибавить 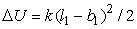 . В программе [2] перебираются материальные точки
. В программе [2] перебираются материальные точки 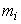 , случайным образом изменяются их координаты и каждый раз вычисляется получающееся значение потенциальной энергии системы. Если при смещении
, случайным образом изменяются их координаты и каждый раз вычисляется получающееся значение потенциальной энергии системы. Если при смещении 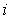 –ой частицы потенциальная энергия уменьшилась, то это новое состояние системы принимается, иначе –– отвергается. Результаты вычислений –– на рис. 1.
–ой частицы потенциальная энергия уменьшилась, то это новое состояние системы принимается, иначе –– отвергается. Результаты вычислений –– на рис. 1.
Задача 2.Имеется неоднородная цепь, ее концы закреплены в фиксированных точках. К заданной точке цепи привязана невесомая нить, которая перекинута через неподвижный блок и соединена с грузом известной массы 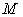 . Требуется рассчитать форму нити. Решение: Заменим цепь совокупностью материальных точек, соединенных пружинами жесткостью
. Требуется рассчитать форму нити. Решение: Заменим цепь совокупностью материальных точек, соединенных пружинами жесткостью 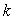 и длиной
и длиной  . Пусть блок имеет небольшие размеры и его координаты равны
. Пусть блок имеет небольшие размеры и его координаты равны 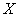 и
и  , а перекинутая через него нить привязана к
, а перекинутая через него нить привязана к 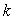 –ой материальной точке с координатами
–ой материальной точке с координатами 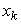 и
и 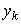 . При расчете потенциальной энергии учтем потенциальную энергию груза массы
. При расчете потенциальной энергии учтем потенциальную энергию груза массы 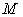 :
: 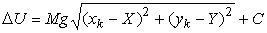 . Если к некоторой
. Если к некоторой 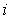 –ой точке цепи привязан груз известной массы
–ой точке цепи привязан груз известной массы 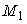 (без блока), то при расчете формы цепи необходимо увеличить массу
(без блока), то при расчете формы цепи необходимо увеличить массу 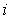 –ой точки на величину
–ой точки на величину 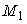 . Во всем остальном задача решается аналогично задаче 1 (программа ПР — 1). Результат решения приведен на рис. 2.
. Во всем остальном задача решается аналогично задаче 1 (программа ПР — 1). Результат решения приведен на рис. 2.
{$N+} uses dos, crt, graph; const N=80; b=5; k=200; g=10; pi=3.1415; { ПР – 1 }
var U,U0,U1,x1,y1,l,dU,S,mm: real; i,j,t,r,Gd,Gm: integer; { Free Pascal }
Energiya: string; x,y,m: array [1..N] of single;
Procedure Energy; var i: integer;
begin U:=0; For i:=2 to N do begin l:=sqrt(sqr(x[i]-x[i-1])+sqr(y[i]-y[i-1]));
If l > b then dU:=k*sqr(l-b)/2; U:=U+dU+m[i]*g*y[i]; end;
S:=sqrt(sqr(x[40]-200)+sqr(y[40]-20)); U:=U+mm*g*S; end;
BEGIN Randomize; Gd:= Detect; InitGraph(Gd, Gm, 'c:\bp\bgi');
For i:=1 to N do begin x[i]:=6*i; y[i]:=-i;
If I < 40 then m[i]:=2 else m[i]:=4; m[20]:=30; end; mm:=25;
Repeat inc(t); For i:=2 to N-1 do begin x1:=x[i]; y1:=y[i]; Energy; U0:=U;
x[i]:=x[i]+random(100)/25-2; y[i]:=y[i]+random(100)/25-2; Energy; U1:=U;
If U1 > U0 then begin x[i]:=x1; y[i]:=y1; end; end; Energy; Str(U,Energiya);
If t mod 500=1 then begin cleardevice;
For i:=1 to N-1 do begin If i < 40 then r:=1 else r:=4;
circle(10+round(x[i]),150-round(y[i]),2); circle(10+round(x[i]),150-round(y[i]),r);
line(10+round(x[i]),150-round(y[i]),10+round(x[i+1]),150-round(y[i+1])); end;
line(10+round(x[40]),150-round(y[40]),200,20); OuttextXY(10,450,Energiya); end;
until KeyPressed; CloseGraph;
END.
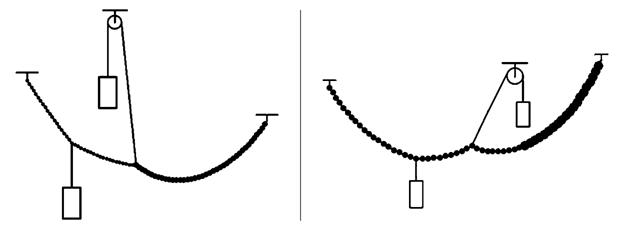
Рис. 2. Результаты вычисления формы нити с грузами в поле тяжести.
Задача 3. Рассчитайте форму упругой пластины, находящейся в однородном поле тяжести. Пластина неоднородная, один ее конец закреплен. Решение: Пластину представим как систему материальных точек 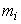 , связанных недеформируемыми стержнями длиной
, связанных недеформируемыми стержнями длиной  . При изгибе пластины изменяются угол
. При изгибе пластины изменяются угол 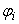 и координаты
и координаты 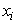 ,
, 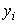 . Потенциальная энергия системы:
. Потенциальная энергия системы:
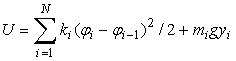 .
.

Рис. 3. Результаты вычисления формы упругой пластины в поле тяжести
В используемой программе [2] реализуется следующий алгоритм. Последовательно перебираются материальные точки 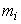 и случайным образом изменяются углы
и случайным образом изменяются углы 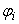 . Каждый раз пересчитывается энергия системы. Если она увеличилась, то эта конфигурация отвергается, а если уменьшилась –– принимается. В результате определяется устойчивое состояние равновесия системы, соответствующее минимуму потенциальной энергии. На рис. 3 представлены результаты расчетов для неоднородного стержня (жесткости левой и правой половин различны), к концу которого прикреплен груз (масса m [N] в 5 раз больше масс других материальных точек).
. Каждый раз пересчитывается энергия системы. Если она увеличилась, то эта конфигурация отвергается, а если уменьшилась –– принимается. В результате определяется устойчивое состояние равновесия системы, соответствующее минимуму потенциальной энергии. На рис. 3 представлены результаты расчетов для неоднородного стержня (жесткости левой и правой половин различны), к концу которого прикреплен груз (масса m [N] в 5 раз больше масс других материальных точек).
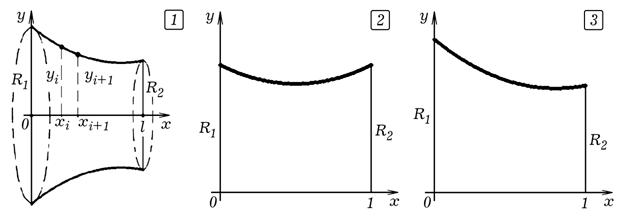
Рис. 4. Форма мыльной пленки, натянутой между двумя кольцами
Задача 4. Имеются два кольца, центры которых лежат на одной оси, перпендикулярной содержащим их плоскостям. Рассчитайте форму натянутой на них мыльной пленки. Решение: Задача состоит в нахождении формы пленки, при которой ее потенциальная энергия, пропорциональная площади 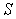 , минимальна. Пленка примет осесимметричную форму, определяемую функцией
, минимальна. Пленка примет осесимметричную форму, определяемую функцией 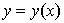 (рис. 4.1). Ее площадь поверхности
(рис. 4.1). Ее площадь поверхности
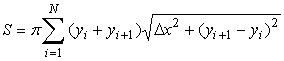 .
.
Используется программа ПР — 2. В процедуре Ploshad осуществляется вычисление площади 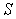 пленки. Затем перебираются все значения
пленки. Затем перебираются все значения  и уменьшаются на 0.0001. При этом каждый раз вычисляется новое значение площади S1. Если площадь уменьшилась, то изменение
и уменьшаются на 0.0001. При этом каждый раз вычисляется новое значение площади S1. Если площадь уменьшилась, то изменение  принимается, а если нет –– отвергается. Все это многократно повторяется, результаты вычислений выводятся в виде графика на экран (рис. 4.2 и 4.3). При слишком малых
принимается, а если нет –– отвергается. Все это многократно повторяется, результаты вычислений выводятся в виде графика на экран (рис. 4.2 и 4.3). При слишком малых 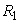 ,
, 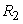 и большом
и большом 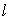 задача не имеет решения.
задача не имеет решения.
{$N+} uses dos, crt, graph; const N=100; R1=1; R2=0.7; pi=3.1415926; { ПР – 2 }
var l,S,dx,a,S0,S1: real; i,j,k,Gd, Gm: integer; y: array[1..N]of single; { Free Pascal }
Procedure Ploshad; begin S:=0; For i:=1 to N-1 do
S:=S+pi*(y[i]+y[i+1])*sqrt(sqr(y[i]-y[i+1])+dx*dx); end;
BEGIN S:=0; dx:=1/N; Gd:=Detect; InitGraph(Gd, Gm, 'c:\bp\bgi');
For i:=1 to N do y[i]:=R1; y[N]:=R2;
Repeat inc(k); For j:=2 to N-1 do begin a:=y[j]; Ploshad; S0:=S; y[j]:=a-0.0001; Ploshad; S1:=S;
If S1>S0 then y[j]:=a; end; If k mod 100=0 then begin cleardevice; line(0,400,640,400);
For i:=1 to 100 do circle(20+round(300*i*dx),400-round(300*y[i]),2); end;
until KeyPressed; CloseGraph;
END.
Задача 5. Рассчитайте форму капли жидкости, лежащей на горизонтальной пластине в поле тяжести Земли. Жидкость частично смачивает пластину. Решение:На жидкость действуют силы тяжести и поверхностного натяжения. Капля принимает форму, при которой ее потенциальная энергия минимальна. Форму капли будем аппроксимировать эллипсоидом вращения вокруг вертикальной оси, нижняя часть которого срезана (рис. 5). Уравнение осевого сечения капли имеет вид:, где
. Площадь всей поверхности капли, включая площадь соприкосновения с пластиной, и ее потенциальная энергия равны:
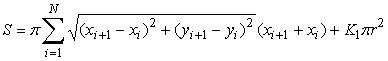 ,
,
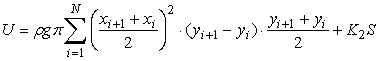 .
.
В программе ПР–3 изменяются параметры 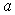 и
и  , а
, а  вычисляется так, чтобы объем капли оставался неизменным. Принимаются такие значения
вычисляется так, чтобы объем капли оставался неизменным. Принимаются такие значения 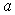 ,
,  и
и  , при которых потенциальная энергия системы минимальна. Меняя
, при которых потенциальная энергия системы минимальна. Меняя 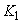 и
и 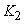 , можно рассчитать форму капли жидкости при различных плотностях, коэффициентах поверхностного натяжения и смачивании поверхности (рис. 5).
, можно рассчитать форму капли жидкости при различных плотностях, коэффициентах поверхностного натяжения и смачивании поверхности (рис. 5).

Рис. 5. Результаты расчета формы капли, лежащей на горизонтальной поверхности
{$N+} uses crt, graph; var k,i, j,DV, MV : integer; { ПР – 3 }
xx,yy,x,y : array[0..205] of extended; r,a1,b1,c1,a,b,c,U,S,V,U1,V0 : real; { Free Pascal }
Procedure Energy; var i: integer;
begin S:=0; V:=0; U:=0; For i:=0 to 200 do begin
y[i]:=c+b-b*i/100; x[i]:=a*sqrt(abs(1-(c-y[i])*(c-y[i])/b/b));end;
For i:=0 to 199 do If y[i]>=0 then begin S:=S+3.14*sqrt(sqr(x[i]-x[i+1])+sqr(y[i]-y[i+1]))*
(x[i]+ x[i+1]); V:=V+3.14*sqr(x[i]+x[i+1])*abs(y[i]-y[i+1])/4; U:=U+3.14*sqr(x[i]+x[i+1]) *(y[i]-y[i+1]) *(y[i]+y[i+1])/8; r:=x[i]; end; S:=S+0.8*3.14*r*r; U:=U+1.2*S; end;
BEGIN DV:=Detect; InitGraph(DV,MV,'c:\bp\bgi'); Randomize;
a:=1; b:=1; c:=b; Energy; U1:=U; V0:=V;
Repeat Energy; a1:=a; b1:=b; c1:=c;
a:=a+0.3*random(100)/100; c:=c+0.3*random(100)/100-0.1; b:=0.1;
Repeat b:=b+0.005; Energy; until V>V0; Energy; k:=0;
If (U>U1) then begin a:=a1; b:=b1; c:=c1; k:=1; end;
If (U<U1) then U1:=U; if k=0 then begin cleardevice;
For i:=0 to 199 do begin y[i]:=c+b-b*i/100; x[i]:=a*sqrt(abs(1-(c-y[i])*(c-y[i])/b/b));
If y[i]>=0 then begin line(320+round(120*x[i]),300-round(120*y[i]),320+round(120*x[i+1]), 300-round(120*y[i+1])); line(320-round(120*x[i]),300-round(120*y[i]),320-round
(120*x[i+1]),300-round(120*y[i+1])); end; end; line(0,300,640,300); end;
until KeyPressed; CloseGraph;
END.
Рассмотренные задачи и их решения могут быть использованы при изучении курсов “Численные методы” и “Компьютерное моделирование”. Автор рекомендует обратиться к электронному пособию “Задачи, алгоритмы, программы” [2].
Литература:
1. Майер Р. В. Компьютерное моделирование физических явлений: Монография. –– Глазов: ГГПИ, 2009. –– 111 с. (http://maier-rv.glazov.net)
2. Майер Р. В. Задачи, алгоритмы, программы: Учебное пособие [Электронный ресурс]. –– Глазов, 2012. (http://maier-rv.glazov.net, http://mayer.hop.ru).
3. Самарский А. А., Вабищевич П. Н., Самарская Е. А. Задачи и упражнения по численным методам: Учеб. пособие. –– М.: Эдиторал УРСС, 2000. –– 208 с.
4. Черноусько Ф. Л., Баничук Н. В. Вариационные задачи механики и управления (Численные методы). –– М.: Наука, 1973. –– 238 с.







