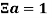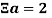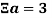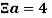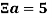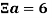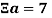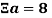- Предисловие
В математике существует понятие цифрового корня и суммы цифр. Работ по данной тематике очень мало. Однако данная работа расширяет это понятие, определяет как действие, вводит новые задачи и обновляет условия уже существующих. Ниже примеры суммы цифр разрядов переопределяют понятие цифрового корня, вводят под общие определения.
- Определение СЦР и КСЦР
Введем понятие — сумма цифр разрядов (далее СЦР). Пусть число представлено в виде:
2.1
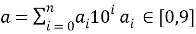
Где n — количество цифр в числе.
Введем символ
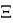
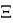
Как пример рассмотрим некое число
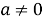
2.2
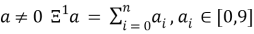
Рассмотрим на примере некоторого числа:
2.3
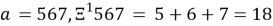
СЦР 2-ого порядка для заданного числа:
2.4
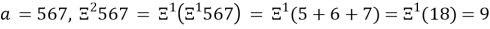
Соответственно СЦР 3-ого порядка будет иметь вид:
2.5
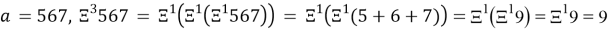
Заметим, если число представлено в виде одной цифры (или n =1), то СЦР 1-ого и любого другого порядка будет равно исходному числу:
2.6
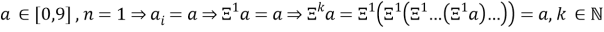
Утверждение выше назовем «Теорема № 1». Если же применять действие сколь угодно много, рано или поздно придем к условию теоремы № 1. Введем действие Конечной Суммы Цифр Разрядом (далее КСЦР). Результат КСЦР всегда будет представлен одноразрядным числом. В противном случае действие СЦР можно будет применять повторно. Для отличия от других действий СЦР, над КСЦР чисел, означающих порядок действия, ставить не будем:
2.7
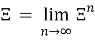
- КСЦР и его свойства
Рассмотрим подробнее действие КСЦР. Так как оно всегда дает результат в виде одноразрядного числа, то КСЦР может принимать значения от 0 до 9. Причем 0 принимает только для 0. Рассмотрим пример и докажем это утверждение. В формулу 2.1 подставим нули. Если число может быть составлено из нулей, то данное формула покажет, как будет выглядеть это число:
3.1
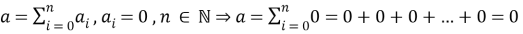
Сумма нулей дает ноль. То есть число, полностью состоящее из нулей, все еще ноль и никакое другое. Следовательно, КСЦР равен нулю только для нуля.
Рассмотрим другие числа. Ниже составим таблицу чисел и значений КСЦР:
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
|
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
|
28 |
29 |
30 |
31 |
32 |
33 |
34 |
35 |
36 |
|
37 |
38 |
39 |
40 |
41 |
42 |
43 |
44 |
45 |
|
46 |
47 |
48 |
49 |
50 |
51 |
52 |
53 |
54 |
Как видно из таблицы, числа чередуются через 9. Предположим, числа чередуются через 9, и тогда удобно число записать как:
3.2
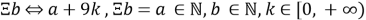
Если это так, то с помощь метода математической индукции докажем истинность этого утверждения:
3.3
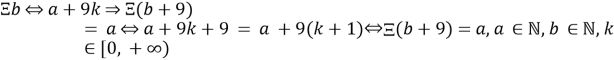
Как видим, при добавлении 9, изменился только порядок, то есть число k. Следовательно, число можно представить в форме остатка деления на 9, за исключением 9. Для удобства и единства записи для 9 будет применяться запись вида:
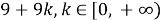
Рассмотрим ряд свойств с КСЦР. Свойство сложения и вычитания:
3.3
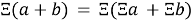
Докажем формулу 3.3. Числа запишем в виде остатка деления на 9:
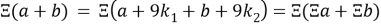
Аналогично будет и для вычитания:
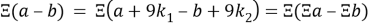
Свойство умножения и деления:
3.4
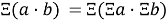
Докажем формулу 3.4. Числа запишем в виде остатка деления на 9:
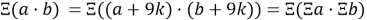
Аналогично и для деления:
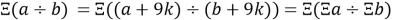
Свойство понижения порядка:
3.5
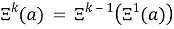
Оно следует из определения порядков в СЦР.
- Последовательности с СЦР и КСЦР
Рассмотрим пару задач, связанных с СЦР и КСЦР. В математике уже есть последовательность A006050 в системе OEIS. Так же есть понятие «Аддитивное постоянство». Или сколько раз надо применять действие СЦР, чтобы действие перешло в КСЦР. Последовательность выглядит следующим образом:
1, 10, 19, 199, 1999999999999999999999,...
На языке данной работы формула последовательности будет задаваться следующим образом:
4.1
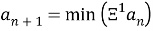
Проверим формулу. Зададим а 1 = 1, тогда следующее наименьшее 10. После десяти наименьшее 19. И так далее.
Как видно формула работает. Однако, вместо 1 можно взять любое другое число и посмотрим, что покажет формула. Для примера начнем с числа 2. Тогда следующим наименьшим числом будет 11, после него 29, затем 2999, и так далее. Ниже распишем таблицу для первых 9 чисел.
|
а 1 = 1 |
10, 19, 199,... |
|
а 1 = 2 |
11, 29, 2999,... |
|
а 1 = 3 |
12, 39, 39999,... |
|
а 1 = 4 |
13, 49, 499999,... |
|
а 1 = 5 |
14, 59, 5999999,... |
|
а 1 = 6 |
15, 69, 69999999,... |
|
а 1 = 7 |
16, 79, 799999999,... |
|
а 1 = 8 |
17, 89, 8999999999,... |
|
а 1 = 9 |
18, 99, 99999999999,... |
Как видно, можно задать любой первый элемент, и дальше последовательность будет строиться на подобии последовательности A006050 в системе OEIS.
Рассмотрим другой случай. Зададим начальное значение a1=20.
Начнем с 20, так как все числа, что указаны в таблице будут повторять уже заданные последовательности.
Последовательность для 20:
20, 299, 2999999999999999999999999999999999, …
Следующее число будет невероятных размеров. Однако, можно вывести формулу общего члена последовательности. Следующий элемент, исходя из поставленного условия, будет состоять из наименьшего количества цифр, чтобы такое количество было наименьшим, необходимо наибольшее количество девяток, причем такая последовательность начинается после 2-ого элемента. Чтобы найти наименьшее количество девяток, достаточно разделить предыдущий элемент на 9. Причем число нацело поделиться на 9, если из него вычесть его же КСЦР. Таким образом — общий вид элемента последовательности:
4.2
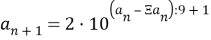
Также, добавляем 1, так как один знак занял КСЦР. И теперь имеем универсальный вид элемента последовательности.
Рассмотрим другую версию данной последовательности. В формуле 4.1 поменяем условие с минимума на максимум:
4.3
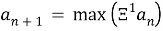
При таком способе задачи общего члена последовательности, уже 2-ой элемент будет настолько невероятных размеров. Что, вероятно, сможет по своим размерам превзойти известное число Грэма или дерево от 3. Однако несмотря на это, в этом числе всего 2 цифры: одна «1» и неисчислимое количество нулей, при условии, что последовательности начинали с 1. То есть a1=1. Тогда следующий элемент выглядит:
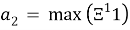
Рассмотрим рекуррентную последовательность на основе СЦР 1-ого порядка:
4.4
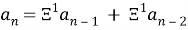
Первые два элемента зададим равными 1 и 1. И составим далее последовательность:
1, 1, 2, 3, 5, 8, 4, 3, 7, 1, 8, 9, 8, 8, 7, 6, 4, 1, 5, 6, 2, 8, 1, 9, 1, 1, 2, 3, 5, 8, 4, 3, 7, 1,8, …
Как видно, последовательность замкнутая, другими словами, числа повторяются в цикле. Для данной последовательности цикл имеет вид:
«1,1,2,3,5,8,4,3,7,1,8,9,8,8,7,6,4,1,5,6,2,8,1,9...»
- Расширение СЦР и КСЦР на вещественные (действительные) и отрицательные
Кроме последовательностей, стоит так же расширить действие на другие виды чисел: вещественные (действительные) и отрицательные.
Начнем с отрицательных чисел. А в частности, целых отрицательных чисел. Так как для целых чисел достаточно сложить только цифры в разрядах. А цифры не могу иметь знаков, кроме положительных. То СЦР любых порядок для отрицательных и положительных чисел равны.
5.1
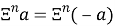
Для вещественных(действительных) чисел разделим действие СЦР на дробную и целую часть. Определим действие СЦР для дробной части:
5.2
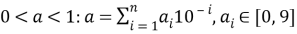
Из чего следует что:
5.3
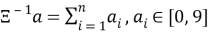
Как видно, формула 5.2 кроме знаков минус, ничем ни отличается от формулы 2.1. А формулы 5.3 и 2.2 идентичны по их определению.
Также введем понятие Полной Суммы Цифр Разрядов (далее ПСЦР). Под ПСЦР будем понимать суммы цифр всех разрядов в вещественном (действительном числе): то есть цифры целой и дробной части:
5.4
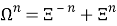
- Заключение
Данная работа только введение в тему. Дает определение и свойства основных действий. Ряд примеров с применением действий СЦР. Данное действие будет очень удобно в решении задач в теории чисел, расчетах и решение математических задач.