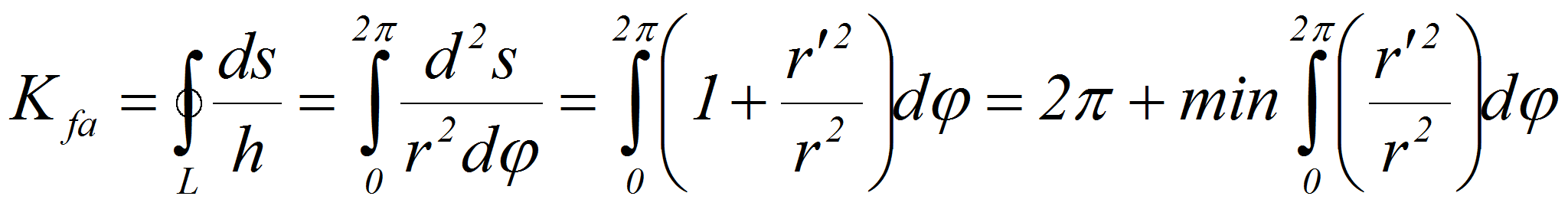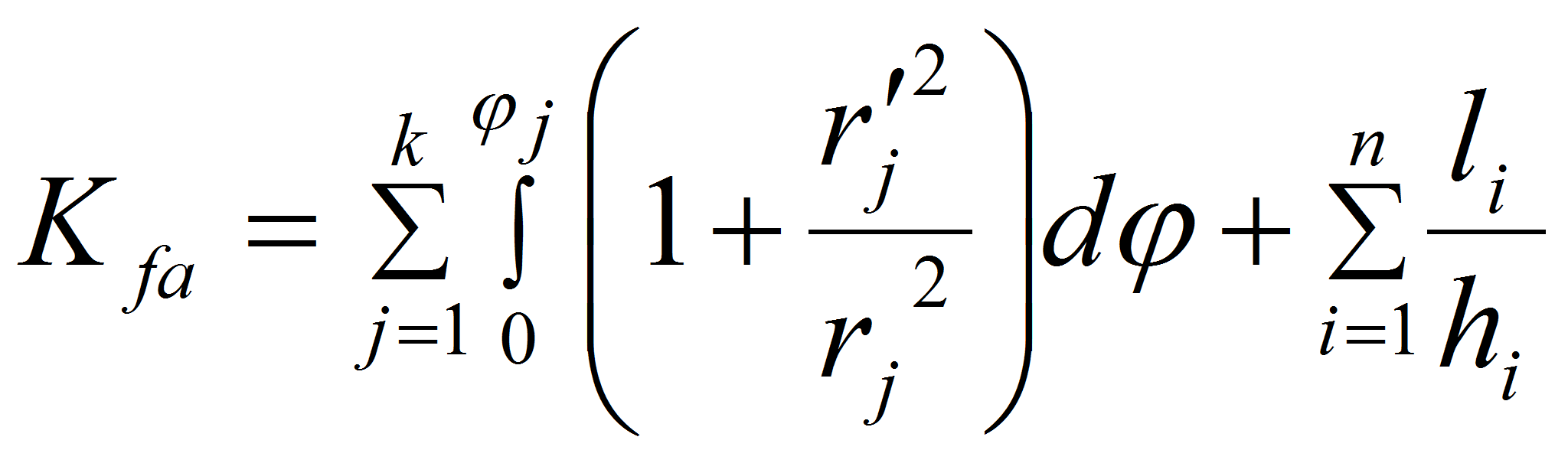The
article in propose form different, which can be applied at comparison
the form
geometry.
В статье идет речь о коэффициенте формы, который может применяться
при сравнении геометрических фигур.
Проектирование современных зданий и сооружений связано с
всесторонними исследованиями прочности и жесткости конструкций,
находящихся под воздействием статистических и динамических нагрузок.
Проблема сравнения разнообразных геометрических фигур широко
представлена в различных отраслях науки и может возникнуть в задачах,
в которых объектом исследования является замкнутая односвязная
область. К этой проблеме приводит и изопериметрическая задача, широко
распространенная в математике, механике сплошных сред, математической
физике, строительной механике мембран, пластинок и оболочек [1].
При сравнении геометрических фигур выбирается критерий сравнения.
Иногда для этого достаточно воспользоваться площадью и периметром
фигур. При сравнении правильных многоугольников в качестве критерия
используется число сторон; при сравнении ромбов – угол между
смежными сторонами и т.д. При сравнении же фигур различных классов,
например, равносторонний треугольник и прямоугольник, выбор критерия
сравнения затруднен. Как показали исследования Д. Пойа и Г. Сеге [2]
во многих прикладных задачах математической физики, в качестве такого
критерия может успешно использоваться интегральная характеристика
формы фигур (коэффициент формы Kf).
Коэффициент формы плоской области является
количественной характеристикой формы области и выражается
через контурный интеграл
-
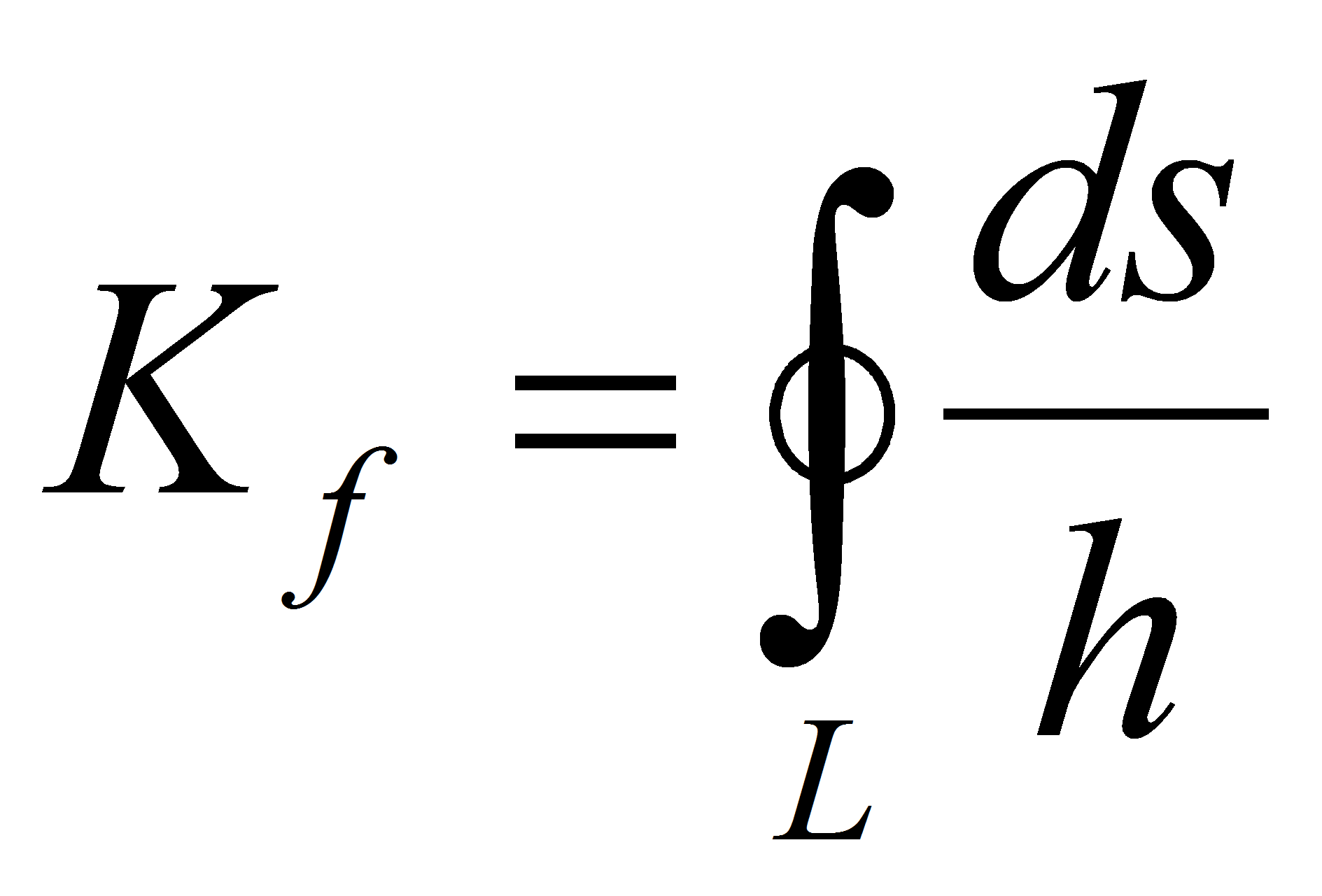 , (1)
, (1)
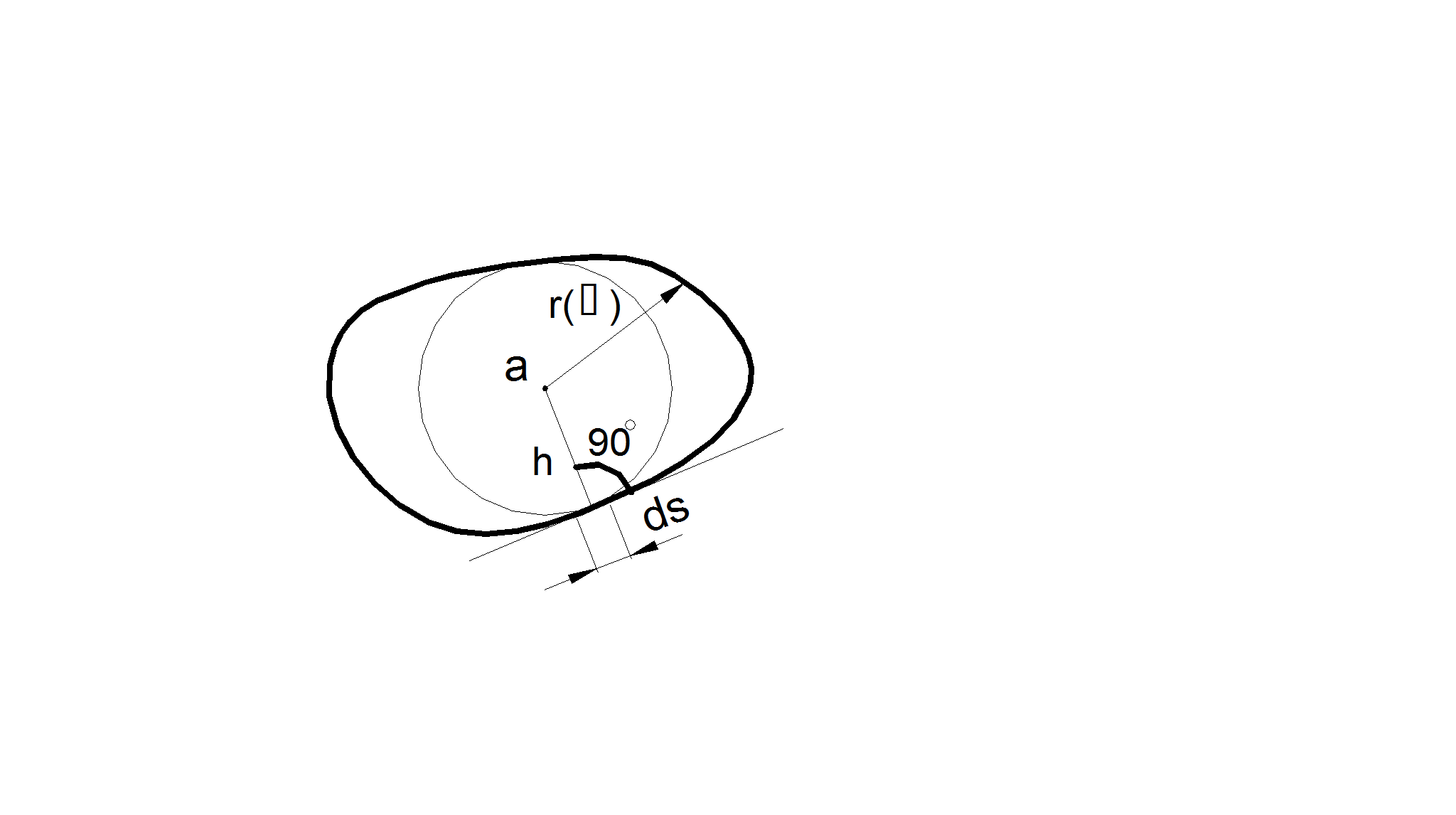
где ds – линейный
элемент контура области (рисунок 1); h
– высота опущенная из полюса, взятого внутри области, на
касательную к переменной точке контура; L
– периметр области. Для фигур с криволинейным контуром
выражение (1) можно преобразовать к следующему виду:
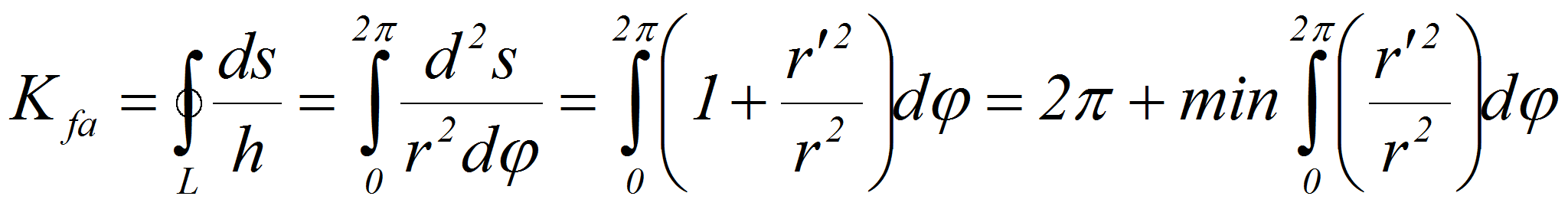 ,
(2)
,
(2)
|
|
|
|
Рисунок 1 |
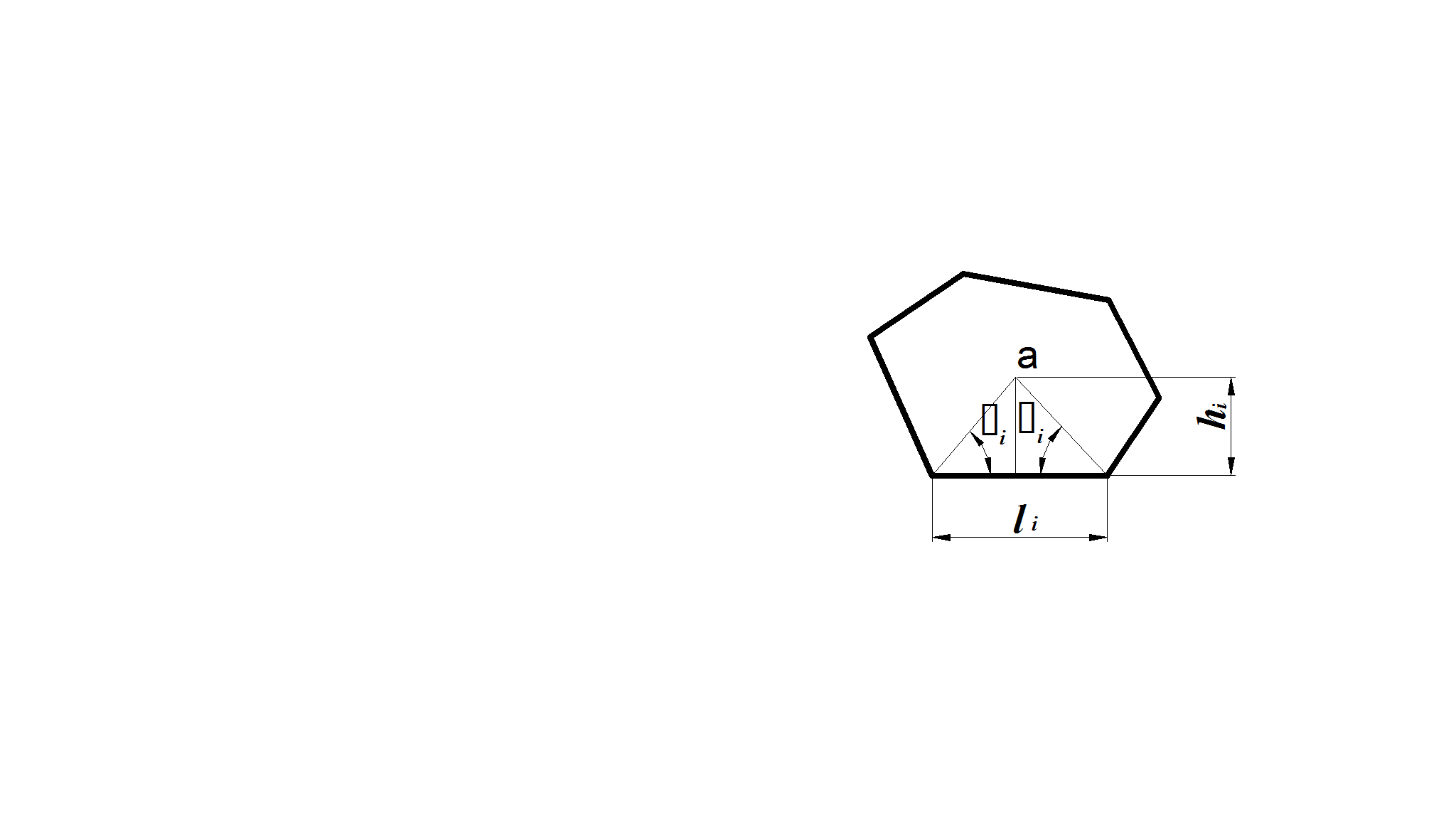
Рисунок 2 |
где r = r(&#;)
- полярное уравнение контура области с полюсом в точке «а».
Из выражения (2) следует теорема 1: из всех плоских фигур наименьшее
значение Kf
= 2π имеет круг, так как для него r′
= 0.
Для областей с полигональным контуром выражение (1) примет вид:
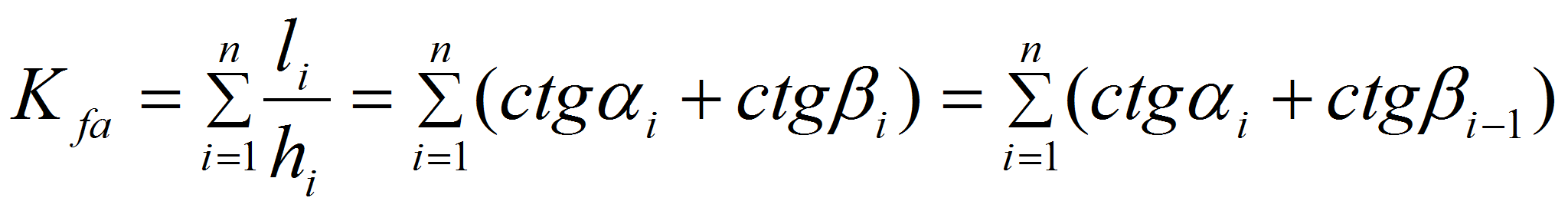 , (3)
, (3)
где li,
hi
длина i-ой стороны многоугольника и
высота, опущенная из полюса на i-ю
сторону (рисунок 2);
 и
и
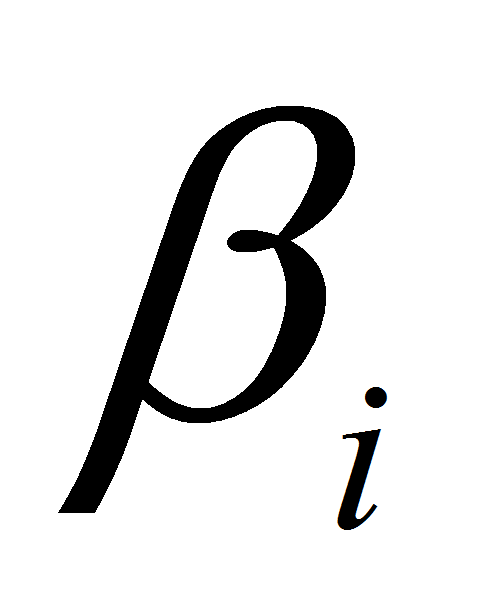 – углы прилежащие к i-той
стороне и ограниченные отрезками прямых, проведенными из полюса в
углы полигона; n – количество
сторон многоугольника.
– углы прилежащие к i-той
стороне и ограниченные отрезками прямых, проведенными из полюса в
углы полигона; n – количество
сторон многоугольника.
Если контур заданной области составлен из криволинейных и
прямолинейных участков, то с учетом выражений (2) и (3) получим:
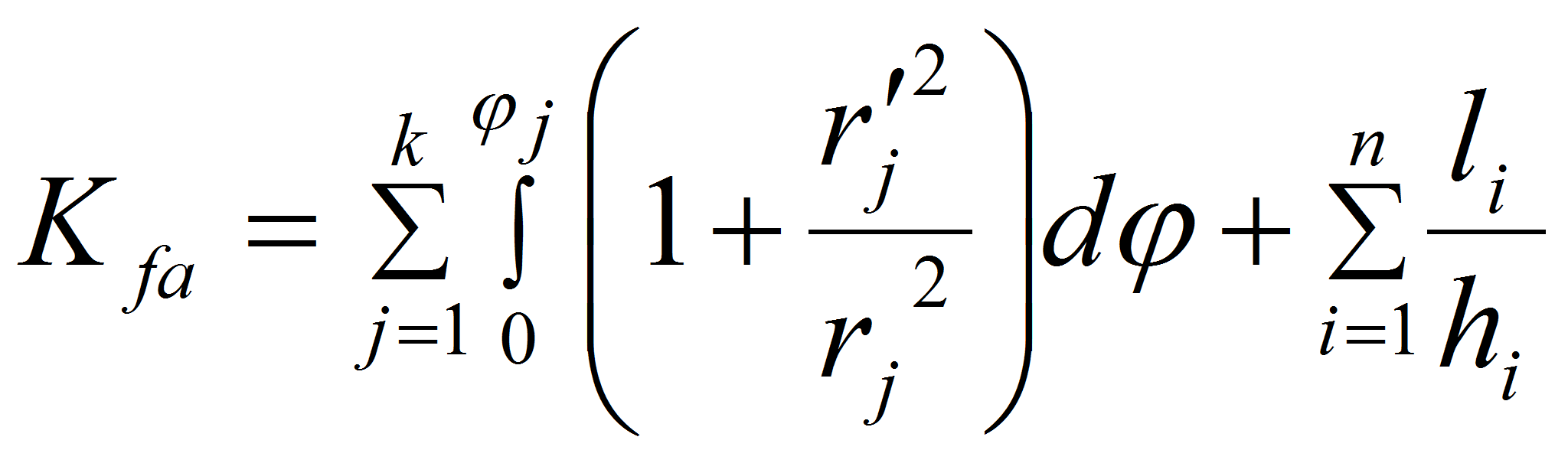 , (4)
, (4)
где k – число криволинейных
участков области, описываемых одной аналитической зависимостью;
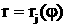 -
полярное уравнение j-го участка
криволинейной части контура, ограничивающий радиусами-векторами j-ый
участок криволинейного контура области.
-
полярное уравнение j-го участка
криволинейной части контура, ограничивающий радиусами-векторами j-ый
участок криволинейного контура области.
Из элементарной геометрии известно, что из всех n-угольников
равной площади А правильный n-угольник имеет наименьший
периметр. Таким образом, из всего множества угольников, все
стороны которых касаются вписанной окружности наименьшее значение Kf
имеет правильный n-угольник.
Как видим и в этом случае для фигур, имеющих центр симметрии, min
Kfa,
достигается тогда, когда точка "а" совпадает с ним.
Обобщая две предыдущие теоремы, можно сформулировать более общую
теорему для n-угольников: из
всего множества n-угольников
наименьшее значение Kf
имеет правильный n-угольник.
Таблица
Коэффициенты формы для различных геометрических фигур
|
Наименование и рисунок фигуры |
Формула |
|
Треугольники
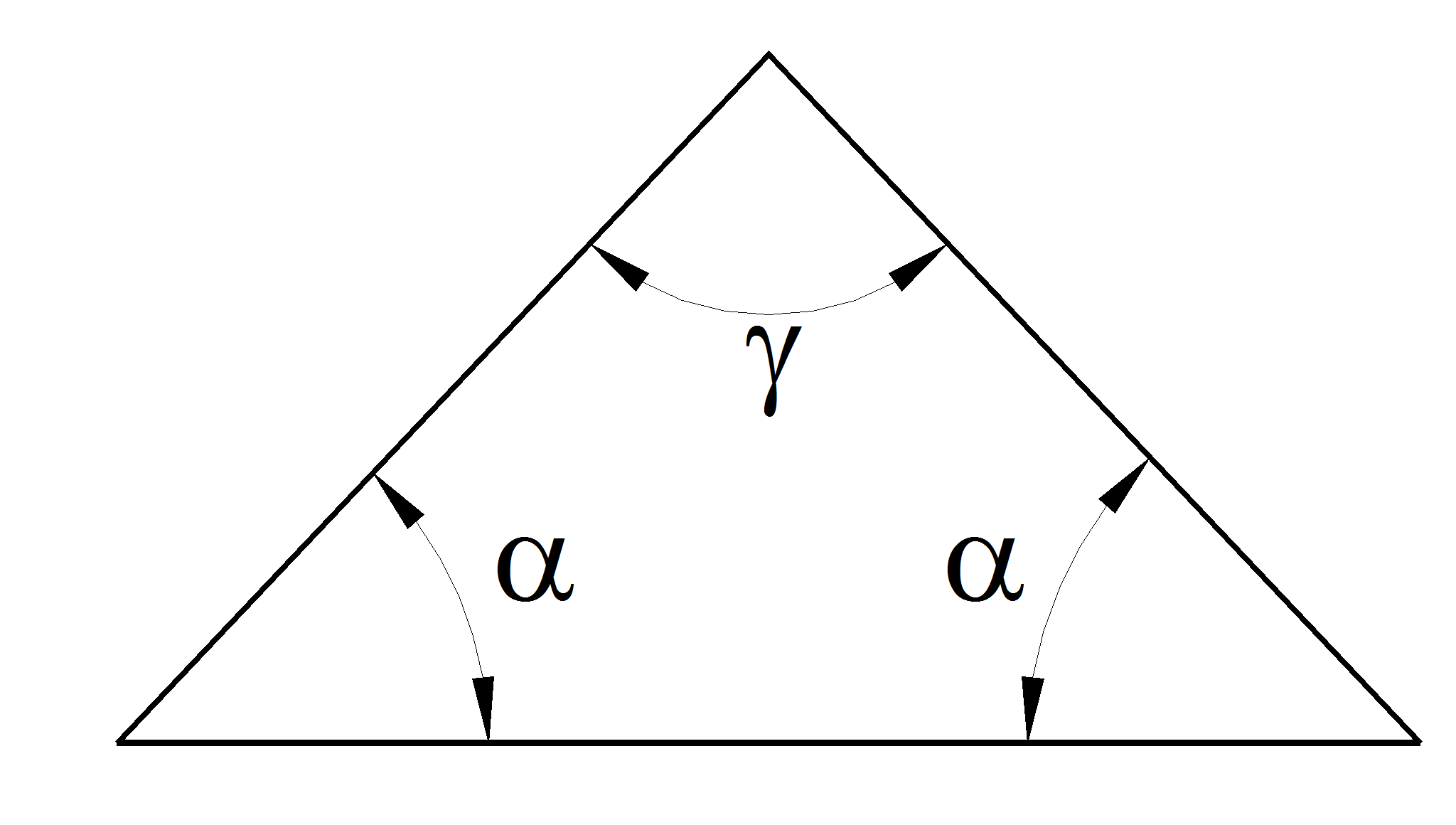
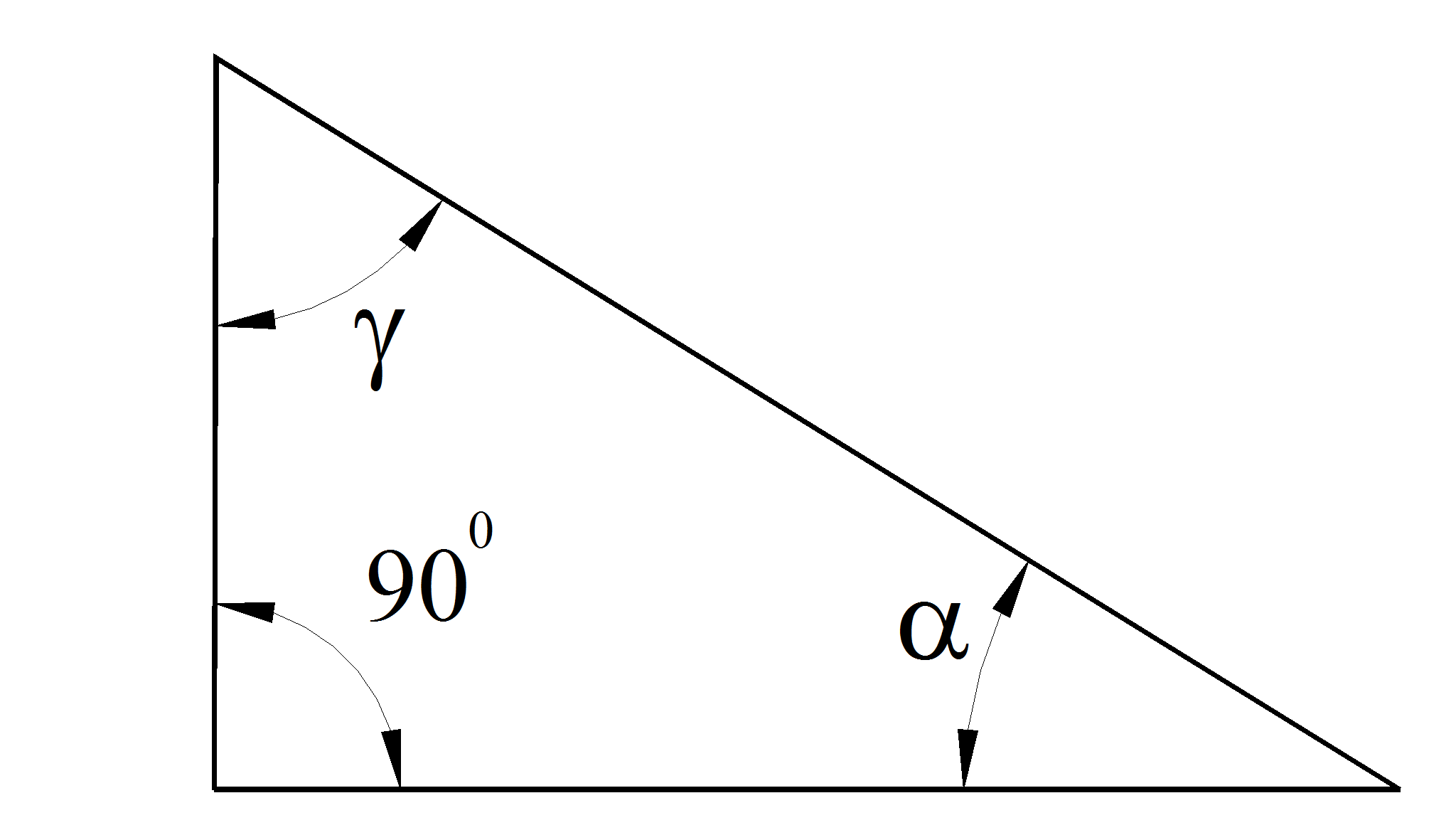 |
Для равнобедренных треугольников:
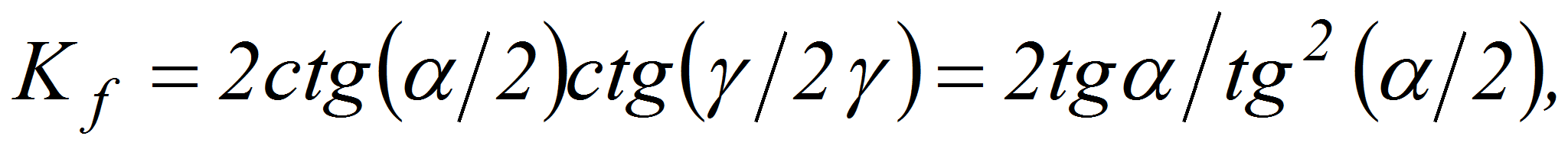
-
где α, γ – углы при вершинах.
-
Для прямоугольных треугольников (β
= 90°):
-
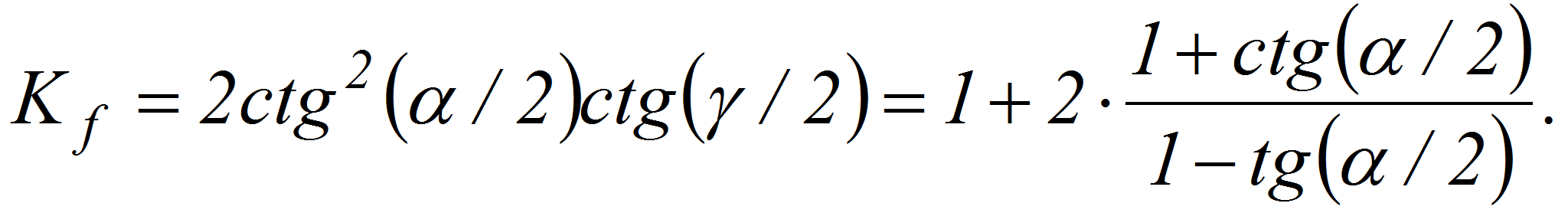
|
|
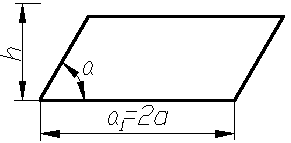
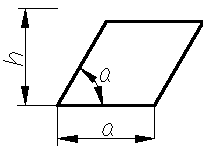
Параллелограммы
|
- Для параллелограмма
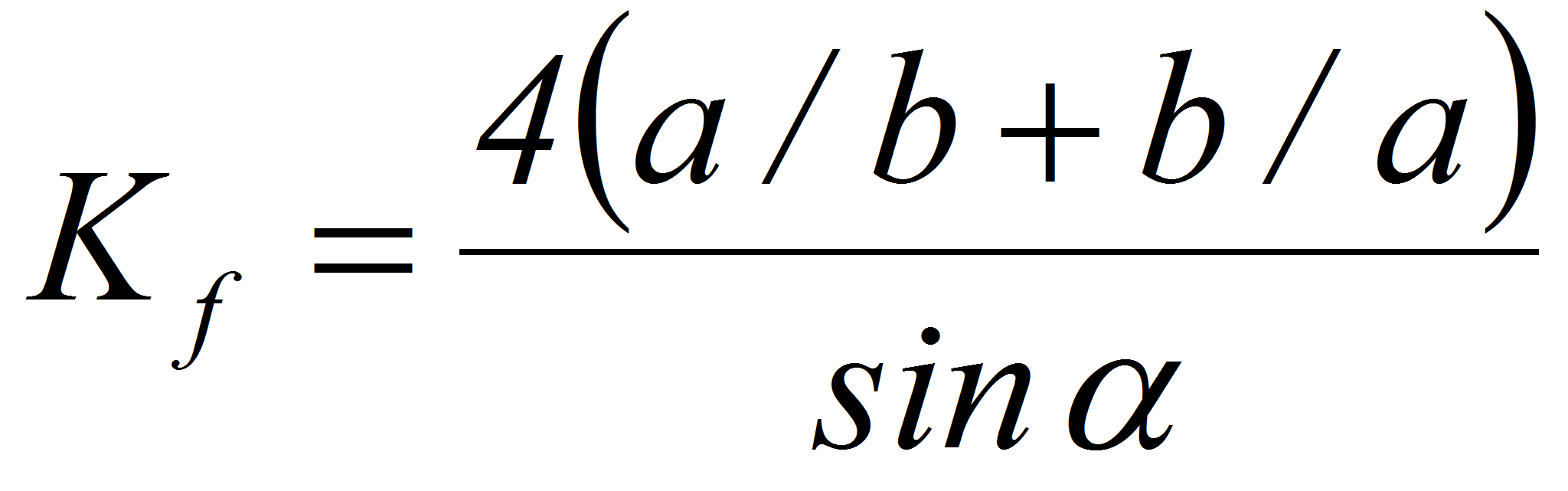
где a, b
– стороны параллелограмма; α – угол при
основании.
-
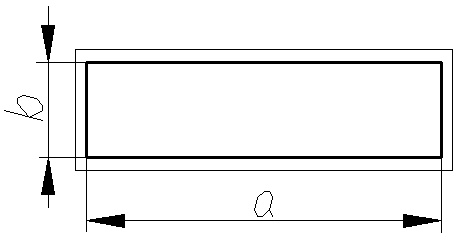
Для прямоугольников:
-
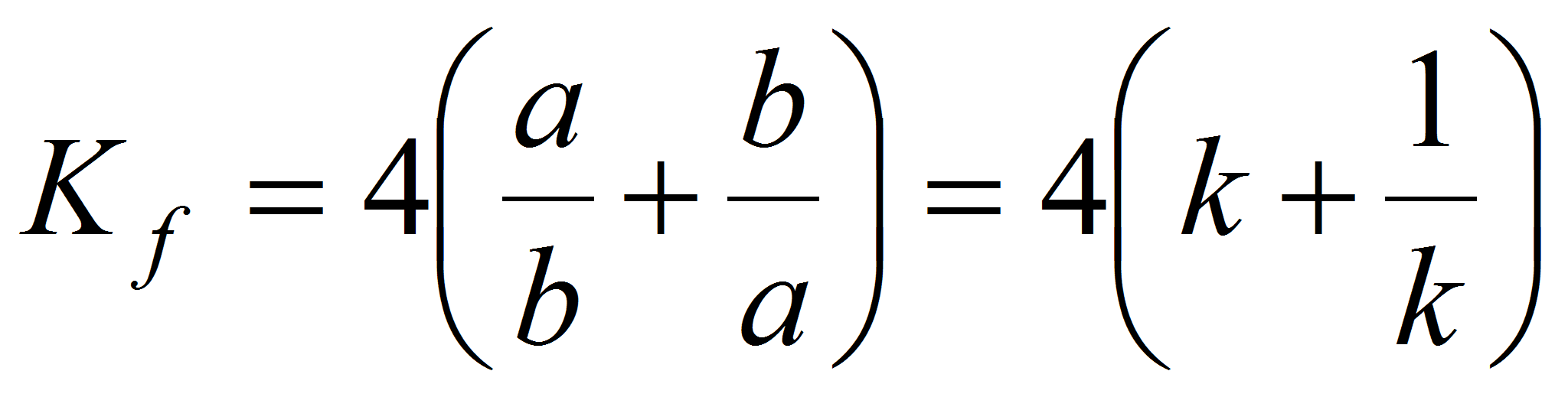 , ,
где a, b
– стороны прямоугольника; k
= a/b.
-
Для ромба:
-
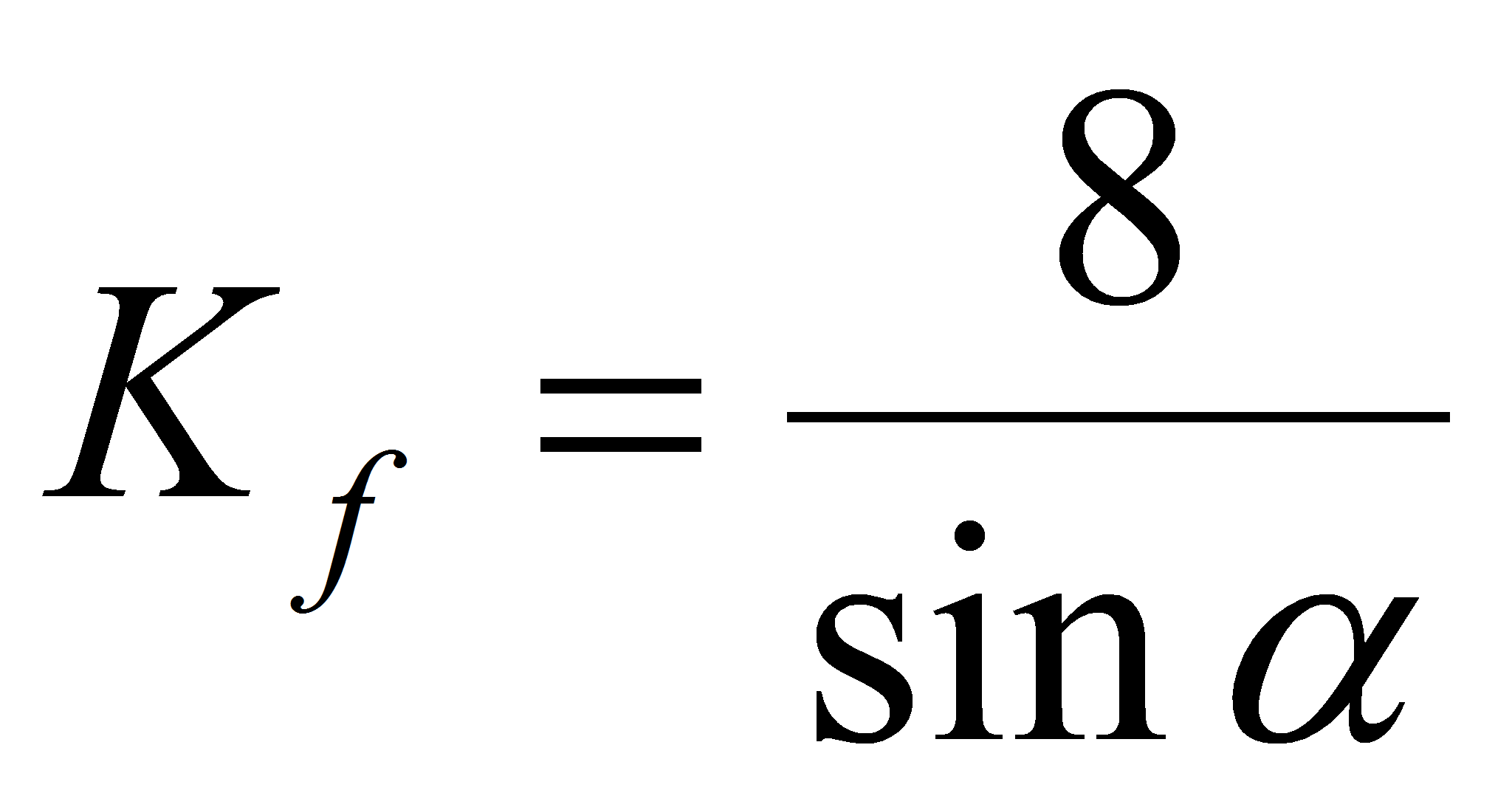 , ,
где α – угол при основании |
|
Трапеции
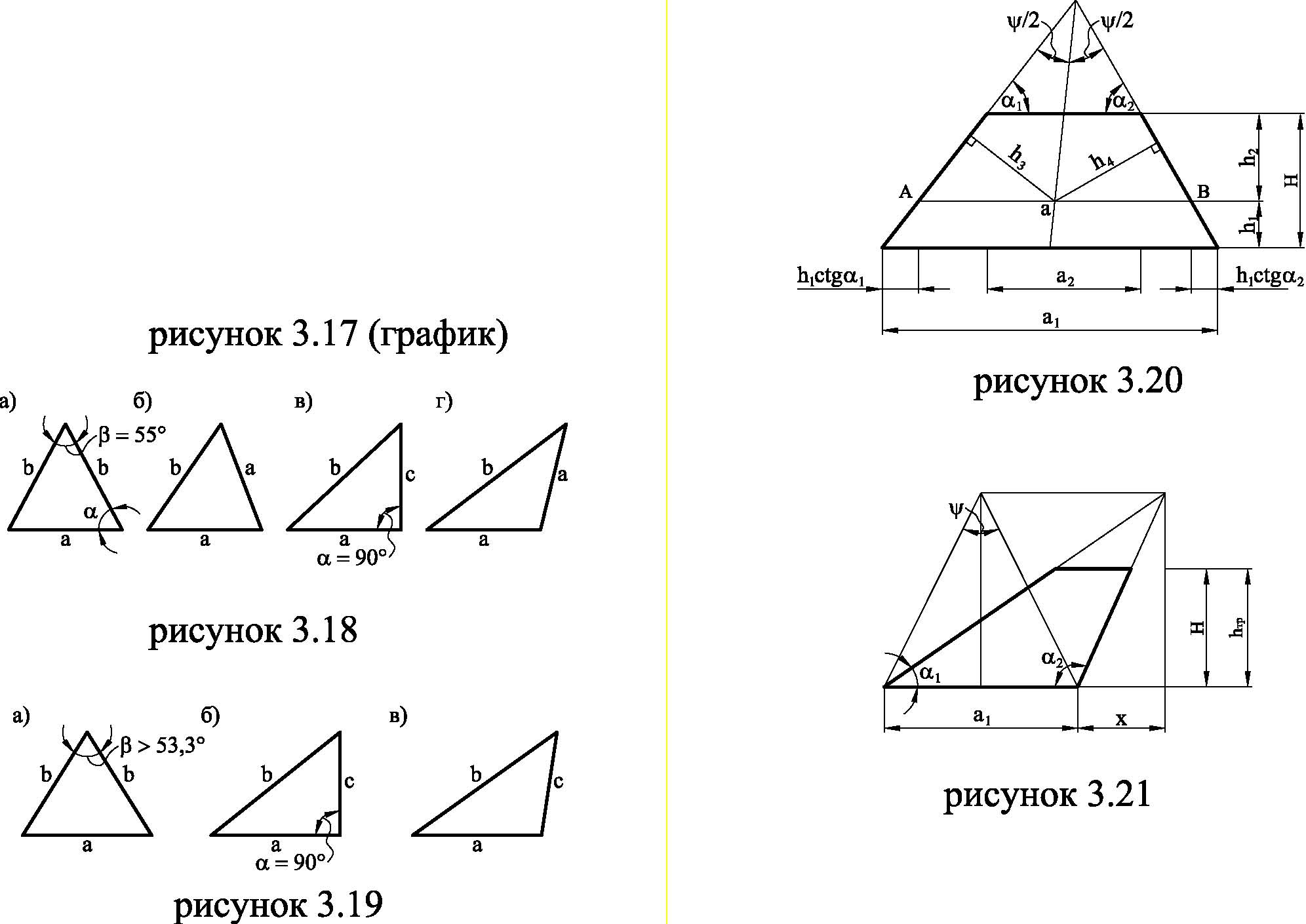 |
- Для равнобочной трапеции (&#;</FONT></I><SUB><I>1</I></SUB><I>
= </I><I><FONT FACE="Symbol">&#;</FONT></I><SUB><I>2 </I></SUB><I>=
</I><I><FONT FACE="Symbol">&#;</FONT></I><I>):</I></DL>
<P>
<A HREF="images/127e35f1.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/127e35f1.gif" NAME="Объект18" ALIGN=ABSMIDDLE WIDTH=409 HEIGHT=48></A>,<P>
где <I>k = a</I><SUB><I>1</I></SUB><I>/a</I><SUB><I>2</I></SUB><SUB>
</SUB> - отношение оснований равнобочной трапеции; <I><FONT FACE="Symbol">&#;</FONT></I>
- угол у основания; <I>K = h</I><SUB><I>1</I></SUB><I>/H</I> –
параметр минимизации.<DL>
<DT>
Для прямоугольной трапеции <I>(</I><I><FONT FACE="Symbol">&#;</FONT></I><SUB><I>1</I></SUB><I>
= 90</I><SUP><I>о</I></SUP><I>, </I><I><FONT FACE="Symbol">&#;</FONT></I><SUB><I>2
</I></SUB><I>= </I><I><FONT FACE="Symbol">&#;</FONT></I><I>)</I>:</DL>
<P>
<A HREF="images/m6381b563.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m6381b563.gif" NAME="Объект19" ALIGN=ABSMIDDLE WIDTH=164 HEIGHT=45></A>.</TD>
</TR>
<TR VALIGN=TOP>
<TD WIDTH=160 STYLE="; border-top: 1px solid #000000; border-bottom: 1px solid #000000; border-left: 1px solid #000000; border-right: none; padding-top: 0cm; padding-bottom: 0cm; padding-left: 0.19cm; padding-right: 0cm">
<P><I>Эллипсы</I><P>
<A HREF="images/2faa39c3.png" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/2faa39c3.png" NAME="Графический объект4" ALIGN=BOTTOM WIDTH=136 HEIGHT=90 BORDER=0></A></TD>
<TD WIDTH=467 STYLE="; border: 1px solid #000000; padding: 0cm 0.19cm">
<P>Для эллипсов:<P>
<A HREF="images/5cf05c80.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/5cf05c80.gif" NAME="Графический объект5" ALIGN=ABSMIDDLE WIDTH=264 HEIGHT=57 BORDER=0></A>,<P>
где <SPAN LANG="en-US"><I>a</I></SPAN> и <SPAN LANG="en-US"><I>b</I></SPAN>
– полуоси эллипса.</TD>
</TR>
</TABLE>
<P>Изопериметрические свойства коэффициента формы:<P>
<I>1. </I><SPAN LANG="en-US"><I>K</I></SPAN><SUB><SPAN LANG="en-US"><I>f</I></SPAN></SUB>
– величина безразмерная и не зависит от масштаба фигур;<P>
<I>2. </I><SPAN LANG="en-US"><I>K</I></SPAN><SUB><SPAN LANG="en-US"><I>f</I></SPAN></SUB>
дает количественную оценку формы геометрических фигур с выпуклым
контуром и может служить критерием для оценки их «правильности»
(«симметричности»);
<P>3. Любая фигура с выпуклым контуром имеет внутри
области единственную точку "а" (центр полярной системы
координат), которая обеспечивает минимальное значение коэффициенту
формы для заданной фигуры (для фигур, имеющих две и более осей
симметрии, точка "а" соответствует их точке пересечения;
для фигур, имеющих одну ось симметрии, точка "а" лежит на
этой оси);<P>
4. Из всех плоских областей наименьшее значение
<I>К</I><SUB><SPAN LANG="en-US"><I>f</I></SPAN></SUB><I>
</I>имеет круг<B>
</B>(<I>К</I><SUB><SPAN LANG="en-US"><I>f</I></SPAN></SUB><SUB><I>
</I></SUB><I> = 2π</I>);<P>
5. Из всех
<SPAN LANG="en-US"><I>n</I></SPAN>-угольников
наименьшее значение <I>К</I><SUB><SPAN LANG="en-US"><I>f</I></SPAN></SUB><SUB><I>
</I></SUB><I> </I>имеет
правильный <SPAN LANG="en-US"><I>n</I></SPAN>
– угольник;
<TABLE WIDTH=676 CELLPADDING=7 CELLSPACING=0>
<COL WIDTH=324>
<COL WIDTH=324>
<TR VALIGN=TOP>
<TD WIDTH=324 STYLE="; border: none; padding: 0cm">
<P><A HREF="images/6edc87b4.jpg" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/6edc87b4.jpg" NAME="Графический объект6" ALIGN=BOTTOM WIDTH=253 HEIGHT=208 BORDER=0></A><P>
Рисунок 3</TD>
<TD WIDTH=324 STYLE="; border: none; padding: 0cm">
<P>6. Значения
<I>К</I><SUB><SPAN LANG="en-US"><I>f</I></SPAN></SUB>
для всего множества плоских областей с выпуклым
контуром, представленных в координатных осях <I>К</I><SUB><SPAN LANG="en-US"><I>f</I></SPAN></SUB><I>
–</I><SPAN LANG="en-US"><I>R</I></SPAN><I>/ρ
</I>(где <SPAN LANG="en-US"><I>R</I></SPAN>
- максимальный радиус вписанной в заданную область
окружности, <I>ρ - </I>минимальный
радиус окружности, описанной вокруг нее) ограничены с двух сторон:
нижнюю границу значений <I>К</I><SUB><SPAN LANG="en-US"><I>f</I></SPAN></SUB>
образуют эллипсы, а верхнюю многоугольники, все</TD>
</TR>
</TABLE>
<P>стороны которых касаются
вписанной окружности, в том числе: правильные многоугольники,
ромбы и треугольники; нижнюю границу значений <I>К</I><SUB><SPAN LANG="en-US"><I>f</I></SPAN></SUB><I>
</I>для всего множества
четырехугольников образуют прямоугольники (рисунок
3).<P>
Последнее свойство коэффициента формы является наиболее важным, оно
имеет большое прикладное значение в методе интерполяции по
коэффициенту формы.<P>
Таким образом, коэффициент формы области является геометрическим
аналогом интегральных характеристик и его использование в качестве
единственного независимого аргумента при построении аппроксимирующих
функций позволяет свести решение сложных физических задач к решению
элементарной геометрической задачи.<P>
<BR />
<P>Литература:
<OL><LI><P>
Коробко, А.В. Геометрическое моделирование формы области в двумерных
задачах теории упругости <FONT FACE="Symbol">&#;</FONT>Текст<FONT FACE="Symbol">&#;</FONT>
/ А.В. Коробко. – М.: Изд-во АСВ, 1999. – 320 с.<LI><P>
Фетисова, М.А. Развитие и применение метода интерполяции по
коэффициенту формы к решению задач поперечного изгиба пластинок с
комбинированными граничными условиями: диссертация ... кандидата
технических наук: 05.23.17 / Фетисова Мария Александровна; [Место
защиты: Орлов. гос. техн. ун-т].- Орел, 2010.- 162 с.: ил.
</OL>
|
![]() и
и
![]() – углы прилежащие к i-той
стороне и ограниченные отрезками прямых, проведенными из полюса в
углы полигона; n – количество
сторон многоугольника.
– углы прилежащие к i-той
стороне и ограниченные отрезками прямых, проведенными из полюса в
углы полигона; n – количество
сторон многоугольника.![]() -
полярное уравнение j-го участка
криволинейной части контура, ограничивающий радиусами-векторами j-ый
участок криволинейного контура области.
-
полярное уравнение j-го участка
криволинейной части контура, ограничивающий радиусами-векторами j-ый
участок криволинейного контура области.