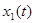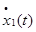Разнообразные задачи геометрии на экстремум площади и объема при заданных ограничениях решались с глубокой древности. Классическая изопериметрическая задача состоит в определении кривой заданной длины, ограничивающей максимальную площадь. К экстремальным задачам геометрии относятся задача Архимеда, в которой требуется среди шаровых сегментов, имеющих заданную площадь поверхности, найти сегмент максимального объема; задача Зенодора, в которой среди n-угольников, имеющих заданный периметр, необходимо найти n-угольник наибольшей площади; задача о геодезической кривой наименьшей длины, лежащей на заданной поверхности, и многие другие. Решение экстремальных геометрических задач важно не только с теоретической, но и практической точки зрения. Такие задачи возникают при раскрое и упаковке промышленных материалов, при размещении грузов на палубах судов и многих других. Рассматриваемые задачи могут быть формализованы и исследованы как задачи оптимального управления [5]. Целью данной работы является разработка численных методов и алгоритмов оптимизации для решения задачи о построении выпуклой пространственной фигуры вращения максимальной площади поверхности при заданных ограничениях на ее ширину.
Плоскость
|
|
(1) |
назовем опорной плоскостью выпуклого множества 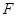 в направлении n, функцию
в направлении n, функцию 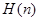 - опорной функцией фигуры
- опорной функцией фигуры 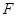 .
.
Введем сферические координаты в трехмерном евклидовом пространстве 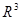 . Тогда
. Тогда 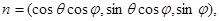
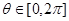 ,
, 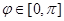 .
.
Положим
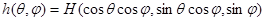 ,
, 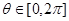 ,
, 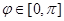 ,
,
и назовем эту функцию опорной функцией фигуры 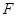 .
.
Определим ширину выпуклой пространственной фигуры 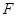 в направлении n:
в направлении n:
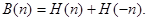
Диаметром выпуклой фигуры 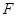 назовем
назовем
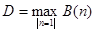 .
.
Толщина выпуклой фигуры 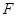 определяется равенством
определяется равенством
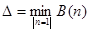 .
.
Опорная функция овала в 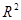 почти всюду на множестве
почти всюду на множестве 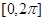 удовлетворяет дифференциальному уравнению:
удовлетворяет дифференциальному уравнению:
|
|
(2) |
где 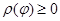 - радиус кривизны границы овала в точке касания P опорной прямой, соответствующей направлению
- радиус кривизны границы овала в точке касания P опорной прямой, соответствующей направлению 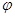 .
.
Опорная функция выпуклой замкнутой регулярной фигуры в 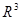 почти всюду на множестве
почти всюду на множестве 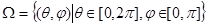 удовлетворяет неравенству:
удовлетворяет неравенству:
|
|
(3) |
Площадь поверхности выпуклой пространственной фигуры определяется выражением:
|
|
(4) |
Опорная функция рассматриваемых фигур удовлетворяет граничным условиям:
|
|
(5) |
Требуется найти выпуклую фигуру вращения, имеющую максимальную площадь поверхности при заданных ограничениях на ее ширину. Поиск фигур осуществляется в классе выпуклых тел вращения с опорной функцией 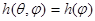 . Обозначим через
. Обозначим через 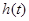 значение опорной функции фигуры в направлении t.
значение опорной функции фигуры в направлении t.
Для фигуры вращения формула (4) имеет вид:
|
|
(6) |
ограничения на ширину:
|
|
(7) |
условия выпуклости:
|
|
(8) |
В заданных направлениях 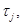
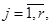 накладываются дополнительные ограничения на ширину:
накладываются дополнительные ограничения на ширину:
|
|
(9) |
где параметры 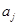 ,
, 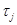 удовлетворяют условиям:
удовлетворяют условиям:
|
|
(10) |
Не ограничивая общности рассмотрения, положим 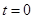 в направлении толщины искомой фигуры:
в направлении толщины искомой фигуры:
|
|
(11) |
Пусть далее 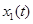 - ширина в направлении t:
- ширина в направлении t: 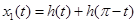 ,
,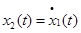 ,
, 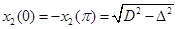 .
.
Задача (6)-(11) формализуется как задача оптимального управления с фазовыми и промежуточными ограничениями:
|
|
(12) |
|
при динамических ограничениях: |
|
|
|
(13) |
|
ограничениях на управление: |
|
|
|
(14) |
|
фазовых ограничениях: |
|
|
|
(15) |
|
промежуточных |
|
|
|
(16) |
|
и граничных условиях: |
|
|
|
(17) |
|
|
(18) |
С использованием метода проекции градиента [6] построено решение задачи при выборе параметров: 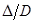 =0,8, q=500 и дополнительном ограничении
=0,8, q=500 и дополнительном ограничении 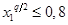 . Результаты численных расчетов приведены на рис.1-5 и в табл.1.
. Результаты численных расчетов приведены на рис.1-5 и в табл.1.
|
|
|
|
|
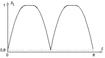
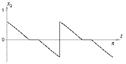
Рисунок 1 - График |
Рисунок 2 - График |
Рисунок 3 - График |
|
|
|
|
|
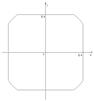
Рисунок 4 - Вид сечения |
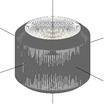
Рисунок 5 - Вид фигуры |
Таблица 1. |
Литература:
1. Andreeva E.A., Klötzler R. Zur analytischen Lösung geometrischer Optimierungsaufgaben mittels Dualität bei Steuerungstheorie // ZAMM. 1984, (64). Teil I. P. 35-44; Teil II. P. 147-153.
2. Андреева Е.А., Цветкова Е.Г., Савичева Ю.А. Решение экстремальных задач геометрии двойственным методом: Учеб. пособие. - Тверь: ТвГУ, 2007.- 180 с.
3. Боннезен Т., Фенхель В. Теория выпуклых тел.- Берлин, 1934.
4. Евтушенко Ю.Г. Методы решения экстремальных задач и их применение в системах оптимизации. М.: Наука, 1982.
5. Кутателадзе С.С., Рубинов А.М. Двойственность Минковского и её приложения.– Новосибирск: Наука, 1976.
6. Трифонов А.Г. Постановка задачи оптимизации и численные методы ее решения, М., Дело, 2002.







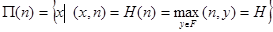
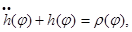
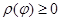 ,
,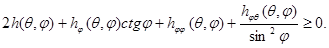
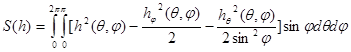 .
.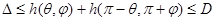 .
.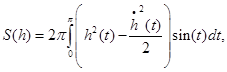
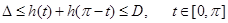 ,
,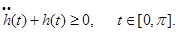
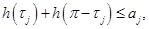
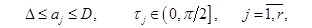
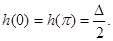
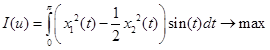 ,
,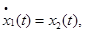
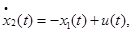
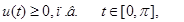
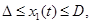
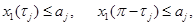
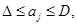
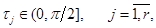
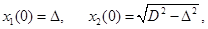
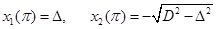 .
.